Verificar as suposições dos modelos é muito importante quando fazemos inferência estatística. Em particular, a suposição de homocedasticidade1 dos modelos de regressão linear é especialmente importante, pois modifica o cálculo de erros padrão, intervalos de confiança e valores-p.
Neste post, vou mostrar três pacotes do R que ajustam modelos da forma
\[ Y_i = \beta_0 + \sum_{k=1}^p\beta_kx_{ik} + \epsilon_i, \ i = 1,\ldots,n\]
\[ \epsilon_{i} \sim \textrm{N}(0,\sigma_i), \ i = 1,\ldots,n \ \textrm{independentes, com }\sigma_i^2 = \alpha x_i^2. \]
Além de mostrar como se faz, também vou ilustrar o desempenho dos pacotes em um exemplo simulado. O modelo que gerará os dados do exemplo terá a seguinte forma funcional
\[ Y_i = \beta x_i + \epsilon_i, \ i = 1,...n \] \[ \epsilon_i \sim N(0, \sigma_i)\text{ independentes, com }\sigma_i = \alpha\sqrt{|x_i|},\]
e os parâmetros do modelo serão os valores \(\beta = 1\) e \(\alpha = 4\). A heterocedasticidade faz com que os pontos desenhem um cone ao redor da reta de regressão.
library(ggplot2)
N <- 1000
set.seed(11071995)
X <- sample((N/100):(N*3), N)
Y <- rnorm(N,X,4*sqrt(X))
qplot(X,Y) +
theme_bw(15) +
geom_point(color = 'darkorange')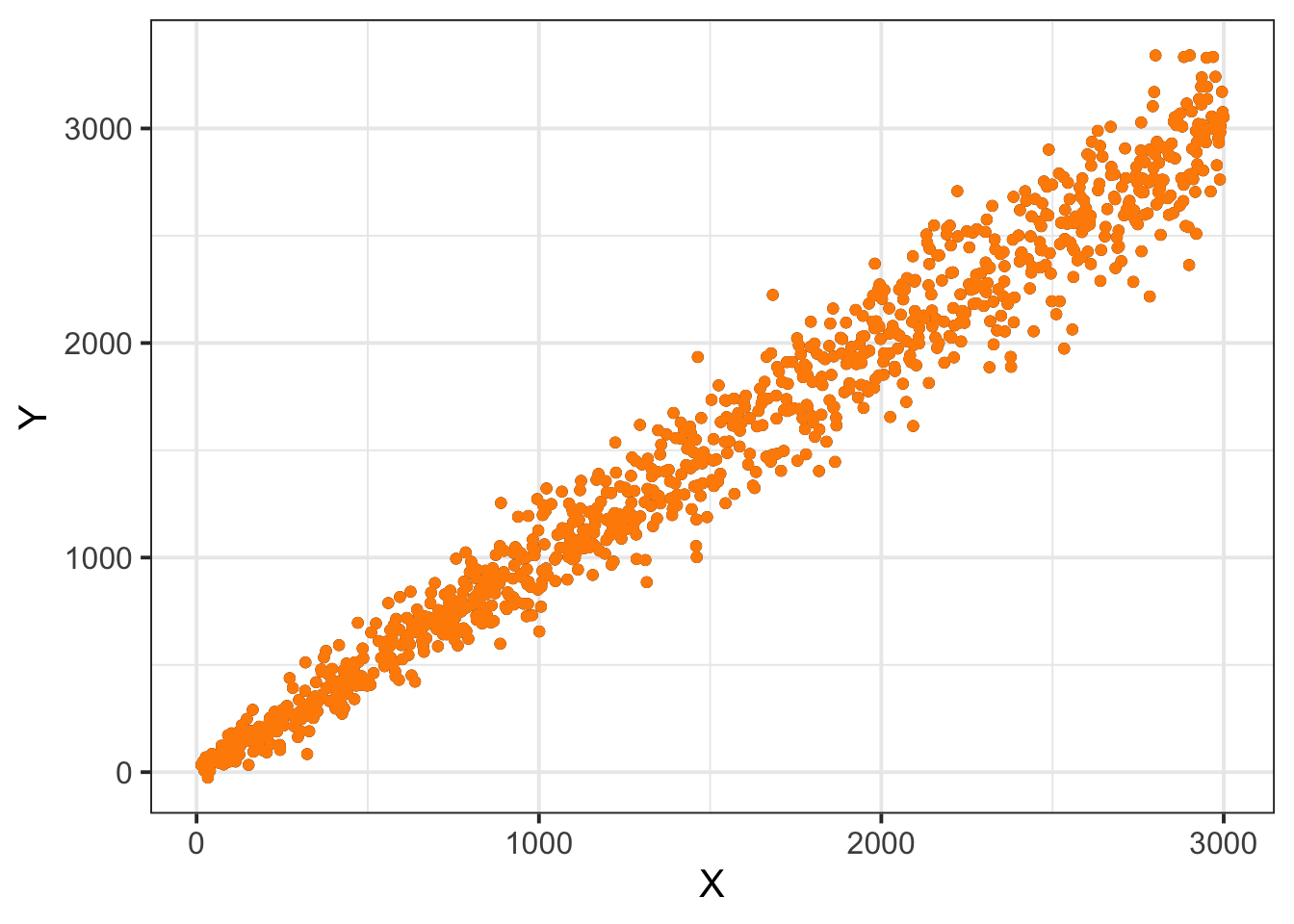
X2 <- sqrt(X)
dataset <- data.frame(Y,X,X2)Usando o pacote gamlss
Quando se ajusta um GAMLSS, você pode modelar os parâmetros de locação, escala e curtose ao mesmo tempo em que escolhe a distribuição dos dados dentre uma grande gama de opções. Escolhendo a distribuição normal e modelando apenas os parâmetros de locação e escala, o GAMLSS ajusta modelos lineares normais com heterocedasticidade.
No código abaixo, o parâmetro formula = Y ~ X-1 indica que a função de regressão será constituída por um preditor linear em X sem intercepto. Já o parâmetro sigma.formula = ~X2-1 indica que o desvio padrão será modelado por um preditor linear em X2 (ou raiz de X), também sem intercepto.
library(gamlss)
fit_gamlss <- gamlss::gamlss(formula = Y ~ X-1,
sigma.formula = ~X2-1,
data = dataset,
family = NO())GAMLSS-RS iteration 1: Global Deviance = 19436.47
GAMLSS-RS iteration 2: Global Deviance = 19412.18
GAMLSS-RS iteration 3: Global Deviance = 19412.18 Conforme descrito no sumário abaixo, a estimativa de alfa está muito abaixo do valor simulado.
summary(fit_gamlss)******************************************************************
Family: c("NO", "Normal")
Call: gamlss::gamlss(formula = Y ~ X - 1, sigma.formula = ~X2 -
1, family = NO(), data = dataset)
Fitting method: RS()
------------------------------------------------------------------
Mu link function: identity
Mu Coefficients:
Estimate Std. Error t value Pr(>|t|)
X 1.029331 0.006297 163.5 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
------------------------------------------------------------------
Sigma link function: log
Sigma Coefficients:
Estimate Std. Error t value Pr(>|t|)
X2 0.190873 0.001025 186.3 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
------------------------------------------------------------------
No. of observations in the fit: 1000
Degrees of Freedom for the fit: 2
Residual Deg. of Freedom: 998
at cycle: 3
Global Deviance: 19412.18
AIC: 19416.18
SBC: 19426
******************************************************************Usando o pacote dglm
Quando se ajusta um Modelo Linear Generalizado Duplo (MLGD em português e DGLM em inglês), você tem uma flexibilidade parecida com a de um GAMLSS. Entretanto, você não pode definir um modelo para a curtose e a classe de distribuições disponível é bem menor.
O código abaixo, similar ao utilizado para ajustar o GAMLSS, ajusta um DGLM aos dados simulados.
library(dglm)
fit <- dglm(Y~X-1, dformula = ~X2-1,data = dataset, family = gaussian, method = 'reml')Warning: glm.fit: algorithm did not convergeNovamente, verifica-se que o alfa estimado está muito distante do verdadeiro alfa.
summary(fit)
Call: dglm(formula = Y ~ X - 1, dformula = ~X2 - 1, family = gaussian,
data = dataset, method = "reml")
Mean Coefficients:
Estimate Std. Error t value Pr(>|t|)
X 1.029142 0.0117601 87.51128 0
(Dispersion Parameters for gaussian family estimated as below )
Scaled Null Deviance: 17738.57 on 1000 degrees of freedom
Scaled Residual Deviance: 3550.323 on 999 degrees of freedom
Dispersion Coefficients:
Estimate Std. Error z value Pr(>|z|)
X2 0.3808943 0.001147175 332.0279 0
(Dispersion parameter for Gamma family taken to be 2 )
Scaled Null Deviance: 1571.507 on 1000 degrees of freedom
Scaled Residual Deviance: 7918.216 on 999 degrees of freedom
Minus Twice the Log-Likelihood: 19412.35
Number of Alternating Iterations: 22 Usando o pacote rstan
Stan é uma linguagem de programação voltada para descrever e manipular objetos probabilísticos, como por exemplo variáveis aleatórias, processos estocásticos, distribuições de probabilidades etc. Essa linguagem foi projetada para tornar intuitivo e simples o ajuste de modelos estatísticos. Em particular, a forma de descrever modelos bayesianos é bem cômoda.
O stan possui várias interfaces para R. A mais básica é o rstan, que será utilizada aqui. A principal função desse pacote é a função rstan, que possui dois parâmetros básicos:
- um parâmetro
model_code =, que recebe um código que descreve o modelo na linguagemstan. - um parâmetro
data =, que recebe uma lista contendo os inputs do modelo, tais como dados coletados, parâmetros de distribuições a priori, etc.
Embora esse seja o mínimo que a função precisa, também podemos passar outras componentes. O parâmetro verbose = FALSE faz com que a função não imprima nada enquanto roda e o parâmetro control = list(...) passa uma lista de opções de controle para o algoritmo de ajuste.
O retorno da função stan() é um objeto do tipo stanfit, que pode ser sumarizado da mesma forma que outros modelos em R, utilizando a função summary() e a função plot().
O código abaixo ilustra a aplicação da função stan() ao nosso exemplo.
library(rstan)
scode <- "data {
int<lower=0> N;
vector[N] y;
vector[N] x;
}
parameters {
real beta;
real<lower=0> alpha;
}
model {
beta ~ normal(0,10);
alpha ~ gamma(1,1);
y ~ normal(beta * x, alpha * sqrt(x));
}"
dados <- list(N = nrow(dataset), y = dataset$Y, x = dataset$X)
fit_stan <- rstan::stan(model_code = scode, verbose = FALSE, data = dados,
control = list(adapt_delta = 0.99))A figura abaixo descreve os intervalos de credibilidade obtidos para cada parâmetro do modelo. O ponto central de cada intervalo representa as estimativas pontuais dos parâmetros. Como se nota, as estimativas do modelo utilizando stan estão bem próximas dos valores verdadeiros.
plot(fit_stan)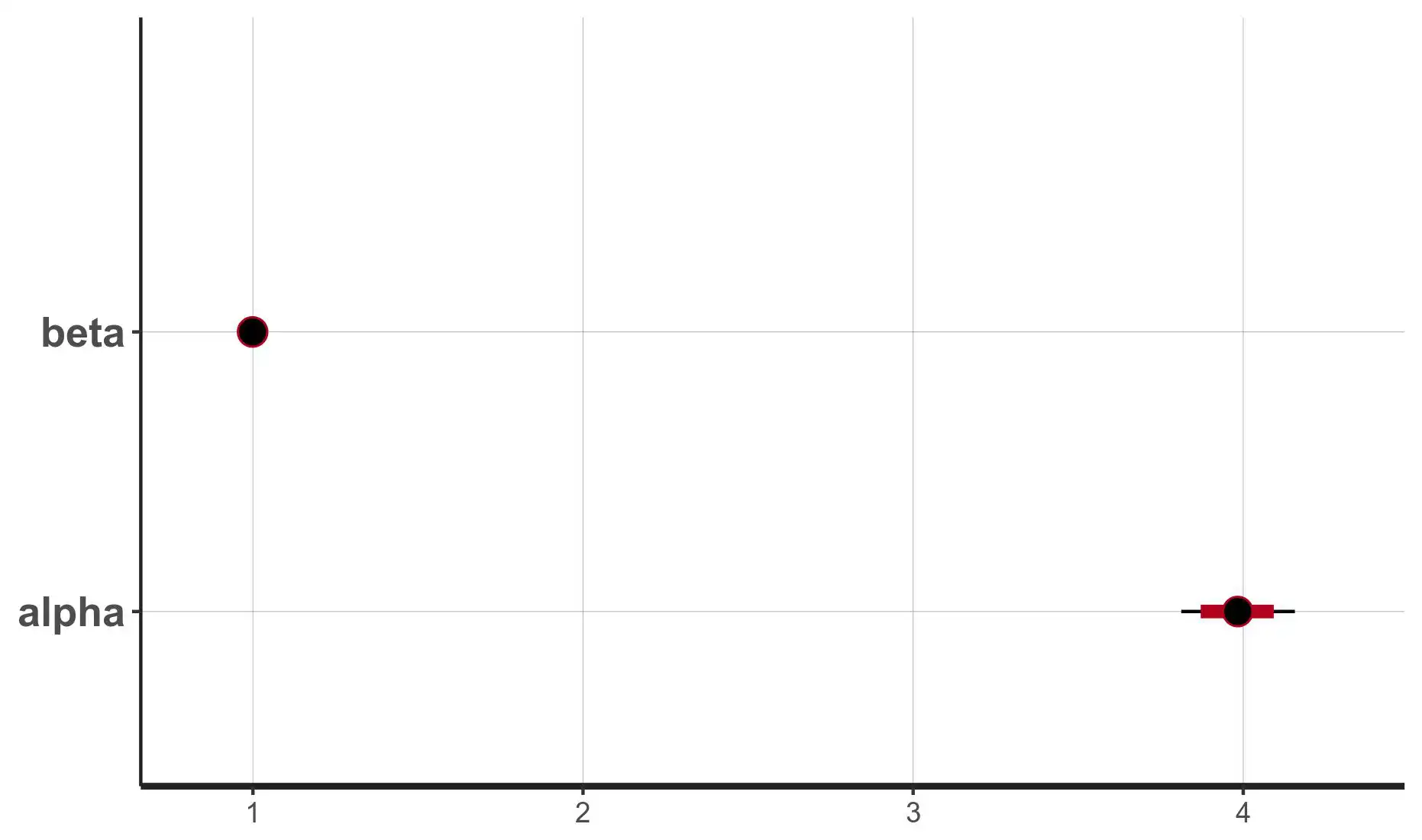
Uma regressão linear é homocedástica quando a variabilidade dos erros não depende das covariáveis do modelo.↩︎


