A distribuição normal (também conhecida como distribuição gaussiana) é um dos conceitos mais importantes da estatística. Ela nos ajuda a interpretar resultados experimentais em todas as áreas da ciência e também é o pressuposto de diversos modelos estatísticos, como por exemplo os modelos de regressão linear.
Nessa série de posts, nós te ajudamos a analisar estatisticamente se uma variável segue ou não a distribuição normal de maneira simples e rápida. Na parte 1 falamos sobre gráficos que podem te ajudar a fazer isso e na parte 2 falamos do pacote PoweR, que concentra uma série de procedimentos estatísticos.
No último post da nossa série vamos falar sobre um ponto muito importante: por que precisamos fazer testes de normalidade? Felizmente, a resposta é simples, mas nem tanto:
Você deve testar a normalidade dos seus dados quando isso for um pressuposto da sua análise
Isso pode parecer óbvio, mas é a coisa mais importante que você precisa saber. Alguns métodos estatísticos funcionam direitinho quando existe uma distribuição normal por trás, como por exemplo a regressão linear simples: os intervalos de confiança têm as propriedades que dizem ter, as estimativas dos betas não terão viés etc. Isso quer dizer que na ausência de normalidade você não deveria usar uma regressão? NÃO! Regressões lineares funcionam bem em muitos contextos, mas se você quiser realizar testes de hipóteses sobre os parâmetros da sua regressão, por exemplo, você pode ter problemas.
Além da regressão linear simples, muitos modelos pressupõem direta ou indiretamente a normalidade dos seus dados, como por exemplo:
- ANOVAs paramétricas (de uma via, duas vias, MANOVA)…
- Regressões lineares simples e múltiplas
- Clusterização por K-médias
Também existem outros procedimentos estatísticos que PODEM precisar que os dados brutos sigam a distribuição normal, mas não vamos falar muito deles pois se o tamanho da amostra for suficientemente grande (\(N\) > 100, por simplicidade) você pode seguir com segurança. Estamos falando de todos os sabores de teste t, por exemplo.
Por que devo testar normalidade depois de fazer uma regressão?
Regressões, bem como ANOVAs, MANOVAs e variações sobre o tema normalmente seguem o seguinte padrão:
\[Y_i = \alpha + \beta X_i+ \epsilon_i \\ \epsilon_i\text{ segue a distribuição normal com média } 0\text{ e variância }\sigma\]
A partir dessa segunda observação sobre a normalidade dos erros, é possível afirmar várias coisas sobre \(\alpha\), \(\beta\) e \(Y_i\): quais são os valores mais prováveis dessas variáveis e quão provável é que eles não sejam 0, por exemplo. Se essas considerações sobre a variabilidade das estimativas te interessam, você deveria testar a normalidade dos resíduos da sua regressão, isso é, a normalidade dos erros \(\hat{Y}_i - Y\) cometidos pelo seu ajuste \(\hat{Y}_i\).
Por que devo testar normalidade depois de ajustar uma clusterização usando o método das k-médias?
Aqui a coisa é um pouco mais feia do que no caso da regressão, mas também é interessante. Uma das maneiras de construir esse algoritmo é assumindo que dentro dos seus dados, sem que você saiba, existe um certo número de distribuições gaussianas. O método das k-médias é perfeito quando essa hipótese é verdadeira: ele é capaz de encontrar perfeitamente esses grupos com um tamanho de amostra suficientemente grande. Mas o que acontece se essa hipótese for falsa?
Um exemplo interessante analisado pelo David Robinson é o caso em que os dados estão distribuídos ao longo de um círculo. A imagem abaixo mostra o que acontece quando rodamos um algoritmo de k-médias nesse conjunto de dados: nós quebramos as esferas/círculos no meio.
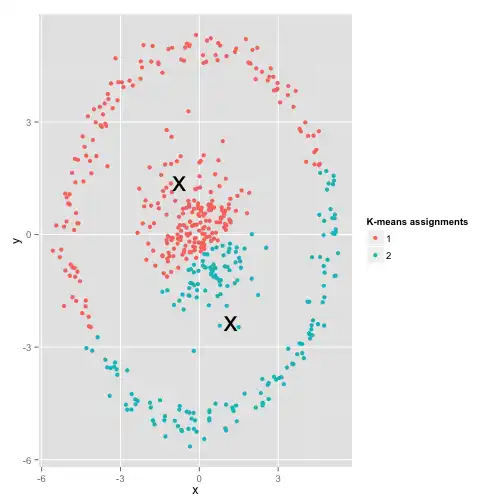
Esquisito né? Os dados de fato se dividem em dois grupos (o círculo de fora e a bola de dentro), o k-médias rodou, mas encontrou grupos diferentes dos “reais”. Essa é uma situação em que usar um teste de normalidade poderia nos dar uma dica de que estamos nesse cenário de desalinho entre o algoritmo utilizado e os dados disponíveis: é muito claro que os grupos encontrados pelo k-médias não seguem uma distribuição normal multivariada. A partir desse teste, poderíamos partir para um outro algoritmo que fosse capaz de encontrar esse padrão, como uma clusterização hierárquica.
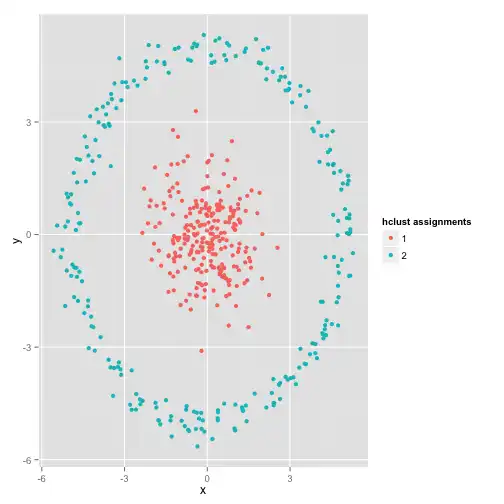
Considerações finais
Lendo esse post você pode estar se perguntando “o algoritmo sempre roda, para qualquer conjunto de dados. para que a normalidade importa?”. De fato, sempre podemos usar todos os algoritmos em todos os contextos, mesmo nos inadequados, e isso não necessariamente é ruim. Com cuidado, você sempre conseguirá interpretar os resultados corretamente e extrair das análises o que for mais útil para você. O que é realmente importante é ter consciência: saber as regras para poder quebra-las, quando for adequado, ou trocar de estratégia quando precisar.
Gostou? Quer saber mais?
Se você quiser aprender um pouco mais sobre esse assunto, temos alguns cursos que tocam os temas deste post. Dê uma olhada nos nossos cursos de Regressão Linear ou Machine Learning e aproveite!


