Mínimos quadrados com restrições lineares

Regressão linear é programação quadrática

Embora seja pouco enfatizado nos bacharelados de estatística, uma regressão linear pode ser formulada como um problema de programação quadrática. Entrando nos detalhes, essa afirmação deve-se a dois fatos:

1. Existe uma teoria, que chama-se programação quadrática, que soluciona problemas da forma

\[\min_x \frac{1}{2}x' Q x + c' x,\]

onde \(x \in \mathbb{R}^p\) e \(Q\) e \(c\) tem dimensões que fazem a conta acima ter sentido. A teoria ocupa-se desenvolvendo algoritmos exatos e aproximados para obter soluções desses problemas, inclusive com generalizações:

\[\min_x \frac{1}{2}x' Q x + c' x, \text{ sujeito a }Ax \geq 0.\]

2. Uma regressão linear consiste em resolver

\[\min_\beta (Y - \beta X)'(Y-\beta X),\]

que, com um pouco de álgebra, é equivalente à

\[ \min_\beta -2Y'X\beta + \beta'X'X\beta.\]

Logo, tomando \(Q = 2X'X\) e \(c = \frac{1}{2}X'Y\) tem-se que esse é um problema de programação quadrática, que por sua vez é um problema convexo, que, segundo a teoria, tem uma única solução no ponto \(\beta = (X'X)^{-1}X'Y\).

Uma regressão linear simples mais flexível

Talvez o jeito mais simples de flexibilizar uma regressão linear no sentido mencionado no começo desse texto é restringir os seus parâmetros. Em muitos contextos, esse é o único jeito de colocar conhecimentos prévios na modelagem¹.

Um caso bastante emblemático aparece nas curvas de crédito divulgadas pela ANBIMA². Lá, ajusta-se um conjunto de curvas que depende de 6 parâmetros e cada curva representa uma classificação de risco (que nem aquela em que o Brasil pode tomar downgrade³). Como os níveis de risco estão ordenados, é natural exigir que também exista uma ordenação entre as curvas. Sem entrar em detalhes, a ideia pode ser expressa assim:

\[\beta_{AAA} < \beta_{AA} < \beta_{A} < \beta_{BBB} < ...\]

O que é que isso tem a ver com programação quadrática? A resposta é que a inequação acima pode ser escrita como \(A\beta \geq 0\), de tal forma já existe uma teoria para resolver uma regressão linear simples com restrições desse tipo! Basta que ela seja vista como um problema de programação quadrática.

O pacote quadprog

Existe um pacote de R para quase tudo, então, como não poderia deixar de ser, existe um pacote em R para resolver problemas do tipo:

\[\min_x \frac{1}{2}x' Q x + c' x, \text{ sujeito a }Ax \geq 0.\]

Para ilustrar o seu uso, vamos considerar um exemplo. Vamos simular um conjunto de dados em que \(\beta_5 = 0.31, \beta_4 = 0.43, \beta_3 = 1.31, \beta_2 = 2.19, \beta_1 = 2.29\) são os valores reais que precisamos estimar, considere que vale

\[Y \approx \beta_1X_1 + \beta_2X_2+\beta_3X_3+\beta_4X_4+\beta_5X_5\]

e que o erro de regressão tem distribuição normal.

set.seed(11071995)
N <- 30

betas <- c(2.29, 2.19, 1.31, 0.43, 0.31)
X <- matrix(rnorm(5*N), byrow = T, ncol = length(betas), nrow = N)
Y <- X %*% betas + rnorm(N, sd = 3)

Se soubermos a priori que valem as seguintes afirmações

\[ \beta_1,\beta_2,\beta_3,\beta_4,\beta_5 > 0 \text{ e } \beta_1 > \beta_2 > \beta_3 > \beta_4 > \beta_5,\]

a minimização de \((Y-\beta X)'(Y-\beta X)\) pode ser resolvida usando a função solve.QP. Tudo que precisamos fazer é escrever o conjunto de inequações na forma \(A\beta \geq 0\). Mas isso é bem fácil! Basta notar que as restrições são equivalentes à

\[ \left(\begin{array}{cccc} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & -1 & 0 & 0 & 0 \\ 0 & 1 & -1 & 0 & 0 \\ 0 & 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 1 & -1 \\ \end{array}\right) \times \left(\begin{array}{c}\beta_1 \\ \beta_2 \\ \beta_3 \\ \beta_4 \\ \beta_5 \end{array}\right) \geq 0.\]

Dessa forma, o problema está prontinho pra passar no moedor de carne, com uma última ressalva. O problema resolvido no solve.QP é

\[\min_x \frac{1}{2}x' Q x + c' x, \text{ sujeito a }A'x \geq 0,\]

então vamos ter que tomar o cuidado de passar as nossas restrições através do transposto da matriz que obtivemos acima. Isso resultará na matriz \(A\).

library(tidyverse)
library(quadprog)

Q <- t(X) %*% X
c <- t(Y) %*% X
A <- cbind(c(1,0,0,0,0),c(0,1,0,0,0),c(0,0,1,0,0),
           c(0,0,0,1,0),c(0,0,0,0,1),c(1,-1,0,0,0),
           c(0,1,-1,0,0),c(0,0,1,-1,0),c(0,0,0,1,-1))

solucao <- solve.QP(Q,  # X'X
                    c,  # Y'X
                    A,  # A transposta
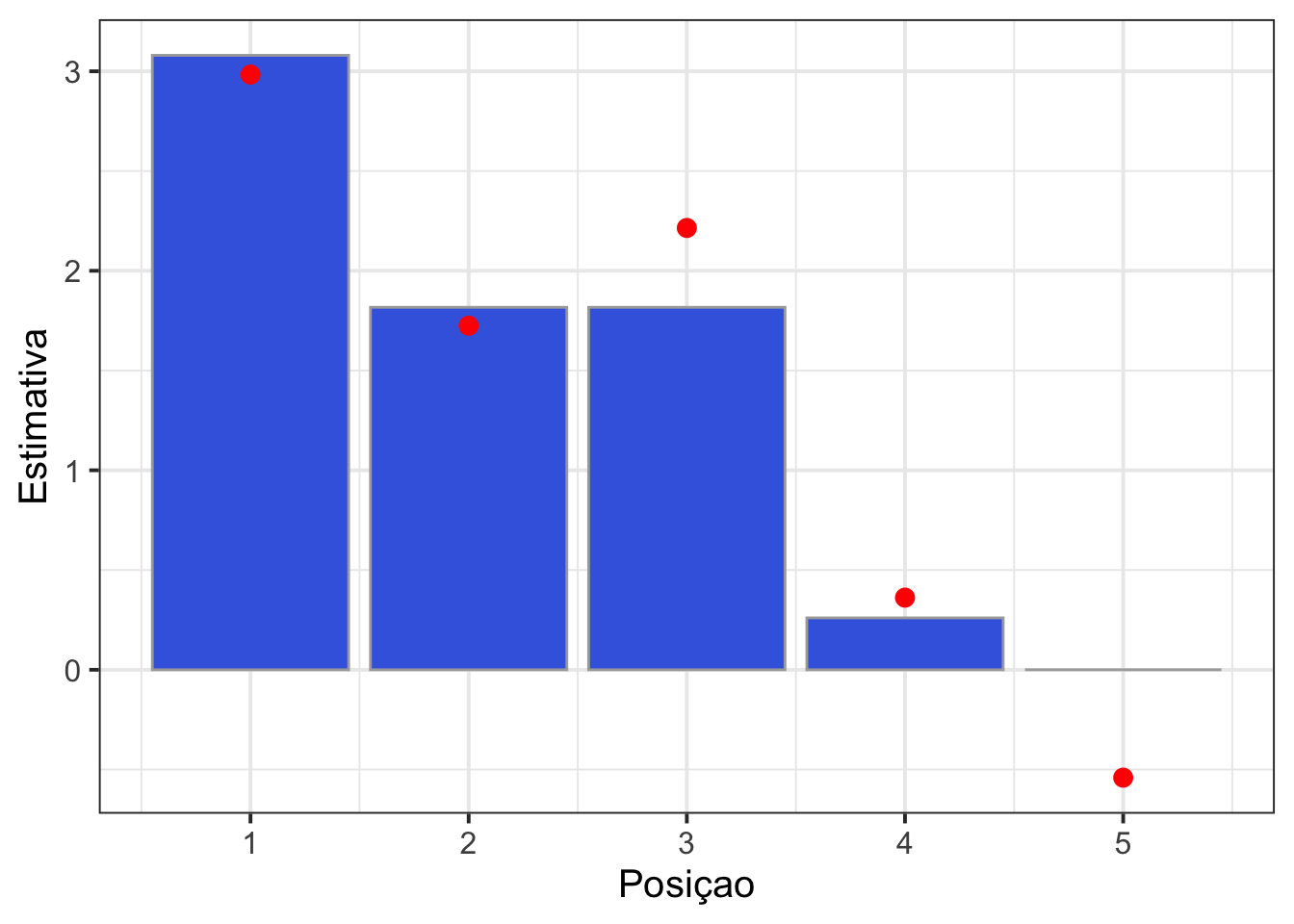
                    c(0,0,0,0,0,0,0,0,0))  # vetor de comparação

Para checar como valeu a pena todo esse esforço, dá uma olhada na diferença entre as estimativas! Os pontinhos vermelhos são as estimativas do modelo irrestrito, enquanto as barras são as estimativas do modelo com restrições.

Conclusões

• Regressão linear simples é um problema de programação quadrática.
• Algumas restrições interessantes podem ser escritas na forma \(B\beta \geq 0\).
• Programação quadrática resolve regressão linear simples com restrições lineares.
• Se em algum dia você topar com um bicho desses, o quadprog pode resolver o problema pra você.