Autoencoders são redes neurais treinadas com o objetivo de copiar o seu input para o seu output. Esse interesse pode parecer meio estranho, mas na prática o objetivo é aprender representações (encodings) dos dados, que podem ser usadas para redução de dimensionalidade ou até mesmo compressão de arquivos.
Basicamente, um autoencoder é dividido em duas partes:
- um encoder que é uma função \(f(x)\) que transforma o input para uma representação \(h\)
- um decoder que é uma função \(g(x)\) que transforma a representação \(h\) em sua reconstrução \(r\)
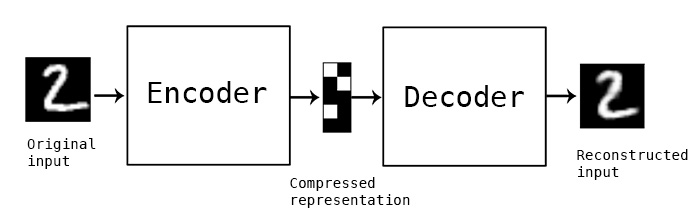 Imagem do blog do Keras
Imagem do blog do Keras
Construindo o seu primeiro autoencoder
Nesse pequeno tutorial, vou usar o keras para definir e treinar os nossos autoencoders.
Como base de dados vou usar algumas simulações e o banco de dados mnist (famoso para
todos que já mexeram um pouco com deep learning). O mnist é um banco de dados de
imagens de tamanho 28x28 de dígitos escritos à mão. Esse dataset promoveu grandes avanços
na área de reconhecimento de imagens.
library(keras)
encoding_dim <- 32
# definindo o input
input <- layer_input(shape = 784)
# definindo o encoder
encoded <- layer_dense(input, encoding_dim, activation = "relu")
# definindo o decoder
decoded <- layer_dense(encoded, 784, activation = "sigmoid")
autoencoder <- keras_model(input, decoded)
encoder <- keras_model(input, encoded)
# definindo o decoder
encoded_input <- layer_input(shape = encoding_dim)
decoder_layer <- autoencoder$get_layer(index = -1L) # última camada do autoencoder
decoder <- keras_model(encoded_input, decoder_layer(encoded_input))Com esse código definimos um modelo da seguinte forma:
\[ X = (X*W_1 + b_1)*W_2 + b_2 \]
Em que:
- \(X\) é o nosso input com dimensão (?, 784)
- \(W_1\) é uma matriz de pesos com dimensões (784, 32)
- \(b_1\) é uma matriz de forma (?, 32)
- \(W_2\) é uma matriz de pesos com dimensões (32, 784)
- \(b_2\) é uma matriz de forma (?, 784)
Note que ? aqui é o número de observaçãoes da base de dados.
Agora vamos estimar \(W_1\), \(W_2\), \(b_1\) e \(b_2\) de modo a minimizar alguma função de perda.
Inicialmente vamos usar a binary crossentropy por pixel que é definida por:
\[-\sum_{i=1}y_i*log(\hat{y}_i)\]
Isso é definido no keras usando:
autoencoder %>% compile(optimizer='adadelta', loss='binary_crossentropy')Não vou entrar em detalhes do que é o adadelta, mas é uma variação do método
de otimização conhecido como gradient descent.
Agora vamos carregar a base de dados e em seguida treinar o nosso autoencoder`.
mnist <- dataset_mnist()
# o mnist é um banco de imagens 28x28, vamos transformar cada imagem em um vetor
# de tamanho 784, cada elemento representado um pixel.
x_train <- mnist$train$x %>% apply(1, as.numeric) %>% t()
x_test <- mnist$test$x %>% apply(1, as.numeric) %>% t()
# vamos transformar as imagens p/ o intervalo 0-1 para que
# a função de perda funcione corretamente.
x_train <- x_train/255
x_test <- x_test/255Estimamos os parâmetros desse modelo no keras fazendo:
autoencoder %>% fit(
x_train, x_train,
epochs = 50,
batch_size = 256,
shuffle = TRUE,
validation_data = list(x_test, x_test)
)Depois de rodar todas as iterações, você poderá usar o seu encoder e o seu decoder
para entender o que eles fazem com as imagens.
Veja o exemplo a seguir em que vamos obter os encodings para as 10 primeiras imagens
da base de teste e depois reconstruir a imagem usando o decoder.
encoded_imgs <- predict(encoder, x_test[1:10,])
dim(encoded_imgs)
encoded_imgs[1,] # representação vetorial de uma imagem.## [1] 10 32
## [1] 0.0000000 10.1513205 3.5742311 2.6635208 6.3097358 3.4840517
## [7] 9.1041250 6.6329145 1.6385922 9.8017225 9.5529270 1.6670935
## [13] 5.7208562 4.8035479 3.9149191 0.6408147 1.2716029 3.1215091
## [19] 13.7575903 0.0000000 1.8692881 3.2142215 0.7444992 5.0728440
## [25] 8.2932110 9.9866810 2.7651572 11.1291723 5.2460670 5.6875997
## [31] 10.6097431 3.6338394O encoder transforma a matriz de (10, 784) para uma matriz com dimensao (10, 2).
Podemos reconstruir a imagem, a pardir da imagem que foi comprimida usando o
nosso decoder.
predict(decoder, encoded_imgs) %>%
split(1:10) %>%
lapply(matrix, ncol = 28) %>%
Reduce(cbind, .) %>%
as.raster() %>%
plot()
Compare as reconstruções com as imagens originais abaixo:
x_test[1:10,] %>%
split(1:10) %>%
lapply(matrix, ncol = 28) %>%
Reduce(cbind, .) %>%
as.raster() %>%
plot()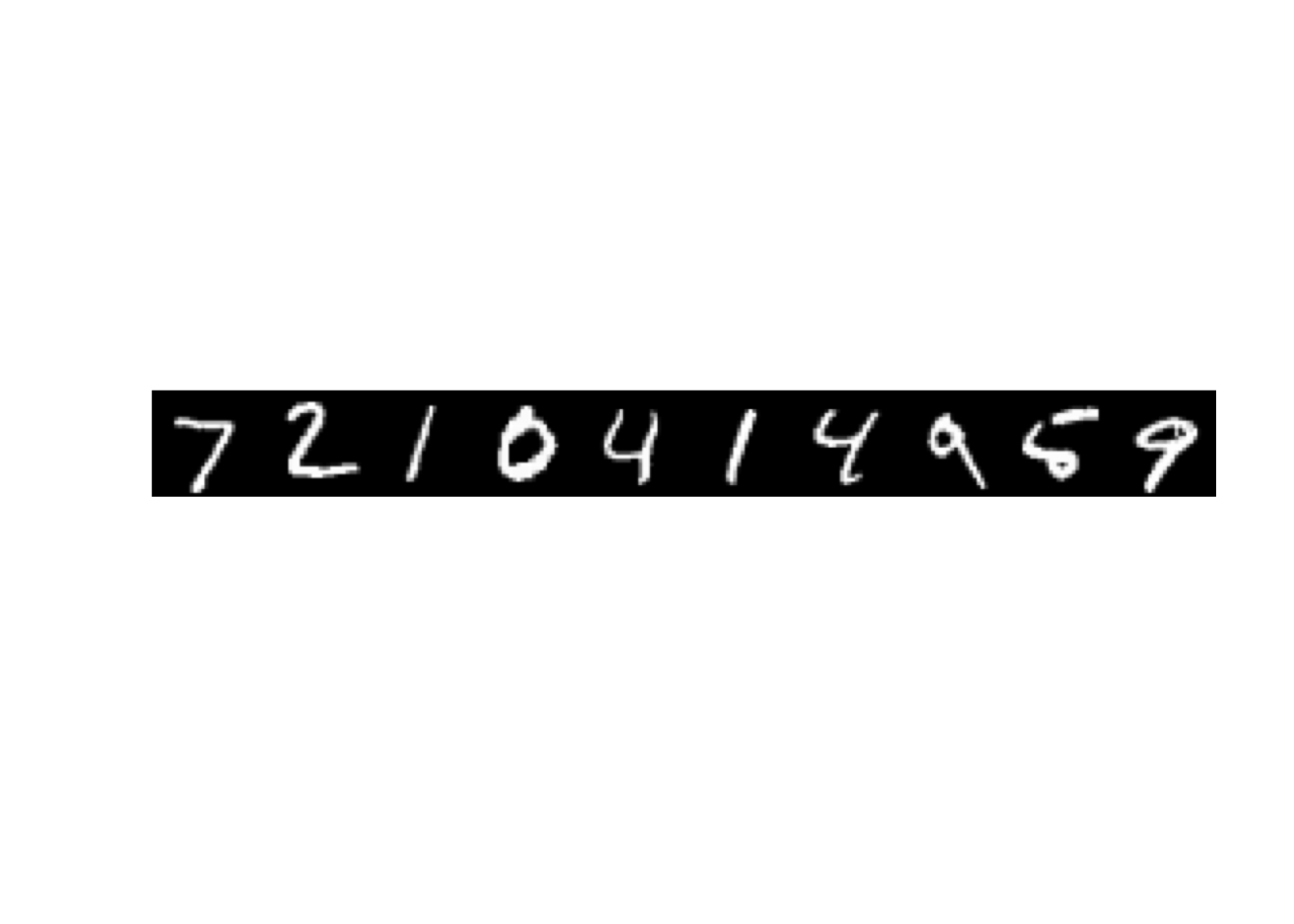
Um ponto interessante é que esse modelo faz uma aproximação da solução por componentes principais! Na verdade, a definição do quanto são parecidos é quase-equivalente. Isso quer dizer que os pesos \(W\) encontrados pelo PCA e pelo autoencoder serão diferentes, mas o sub-espaço criado pelos mesmos será equivalente.
Se são equivalentes, qual a vantagem de usar autoencoders ao invés de PCA? O PCA para por aqui, você define que serão apenas relações lineares, e você reduz dimensão apenas reduzindo o tamanho da matriz. Em autoencoders você tem diversas outras saídas para aprimorar o método.
A primeira delas é simplesmente adicionar uma condição de esparsidade nos pesos. Isso vai reduzir o tamanho do vetor latente (como é chamada a camada do meio do autoencoder) também, pois ele terá mais zeros.
Isso pode ser feito rapidamente com o keras. Basta adicionar um activity_regularizer
em nossa camada de encoding. Isso vai adicionar na função de perda um termo que
toma conta do valor dos outputs da camada intermediária.
# definindo o input
input <- layer_input(shape = 784)
# definindo o encoder
encoded <- layer_dense(input, encoding_dim, activation = "relu",
activity_regularizer = regularizer_l1(l = 10e-5))
# definindo o decoder
decoded <- layer_dense(encoded, 784, activation = "sigmoid")
autoencoder <- keras_model(input, decoded)
autoencoder %>% compile(optimizer='adadelta', loss='binary_crossentropy')
autoencoder %>% fit(
x_train, x_train,
epochs = 50,
batch_size = 256,
shuffle = TRUE,
validation_data = list(x_test, x_test)
)Outra forma de melhorar o seu autoencoder é permitir que o encoder e o decoder sejam redes neurais profundas. Com isso, ao invés de tentar encontrar transformações lineares, você permitirá que o autoencoder encontre transformações não lineares.
Mais uma vez fazemos isso com o keras:
input <- layer_input(shape = 784)
encoded <- layer_dense(input, 128, activation = "relu") %>%
layer_dense(64, activation = "relu") %>%
layer_dense(32, activation = "relu")
decoded <- layer_dense(encoded, 64, activation = "relu") %>%
layer_dense(128, activation = "relu") %>%
layer_dense(784, activation = "sigmoid")
autoencoder <- keras_model(input, decoded)
autoencoder %>% compile(optimizer='adadelta', loss='binary_crossentropy')
autoencoder %>% fit(
x_train, x_train,
epochs = 50,
batch_size = 256,
shuffle = TRUE,
validation_data = list(x_test, x_test)
)Existem formas ainda mais inteligentes de construir esses autoencoders, mas o post iria ficar muito longo e não ia sobrar asssunto para o próximo. Se você quiser saber mais, recomendo fortemente a leitura deste artigo do blog do Keras e desse capítulo.
Uma família bem moderna de autoencoders são os VAE (Variational Autoencoders). Esses autoencoders aprendem modelos de variáveis latentes. Isso é interessante porque permite que você gere novos dados, parecidos com os que você usou para treinar o seu autoencoder. Você pode encontrar uma implementação desse modelo aqui.
É isso! Abraços


