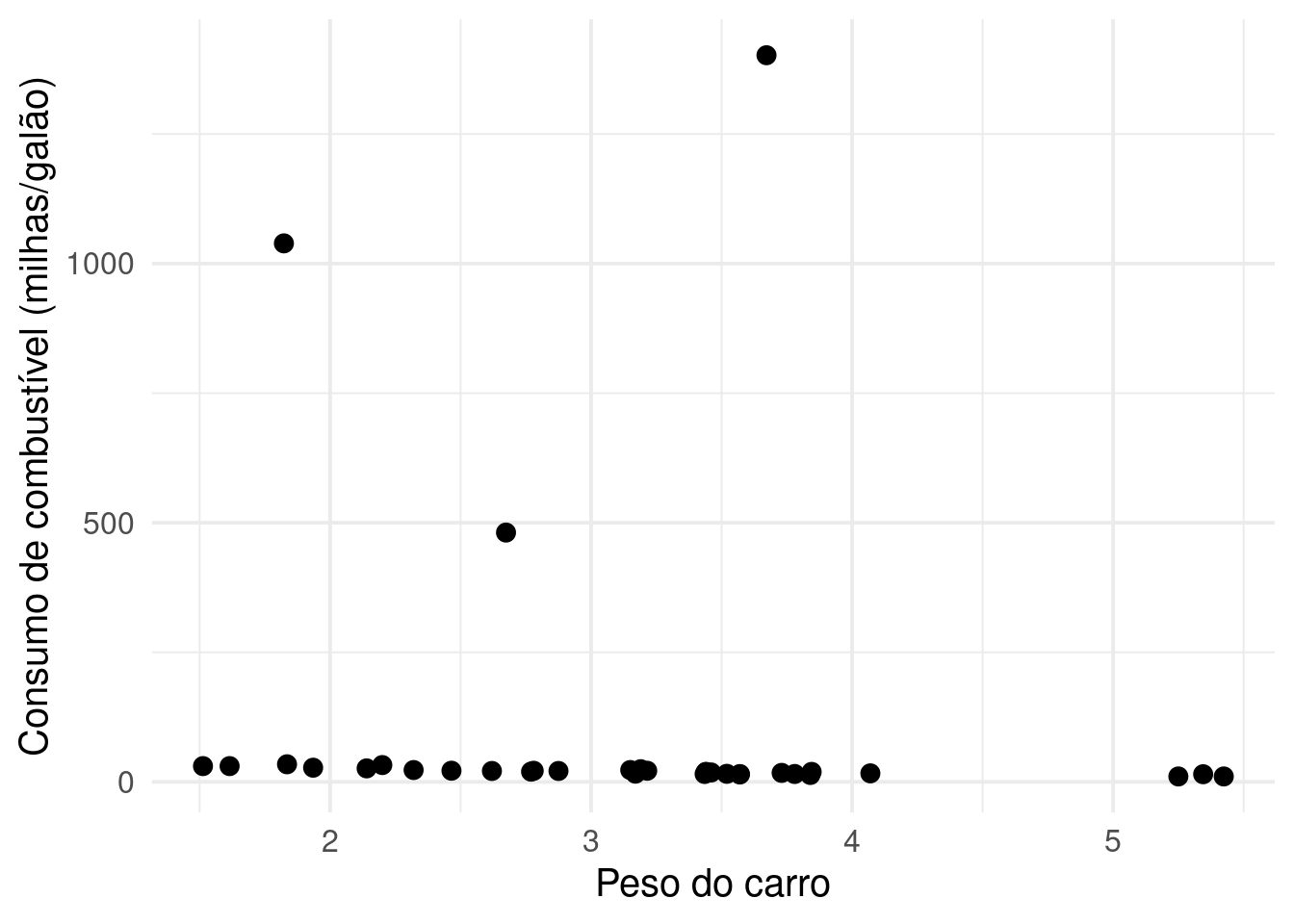
Você já passou pela situação de fazer um gráfico e se deparar com uma imagem triste como essa? Quando você nem sequer consegue ver o que está acontecendo porque um ponto está deixando a sua escala completamente bagunçada?

Esses dados que dificultam a nossa vida normalmente são chamados de outliers ou também de dados discrepantes e pontos fora da curva. Existem muitos jeitos de tratar esse tipo de dados, pois se por um lado ele pode ser um erro da base e deve ser descartado, também existem situações em que os outliers são características importantes dos seus dados e merecem ser compreendidos em profundidade. Hoje, nós vamos falar sobre uma estratégia rápida e fácil que tem o potencial de resolver os seus problemas sem te dar dor de cabeça.

O método mais comum para encontrar outliers usa o famoso z-score, que nada mais é que uma transformação de uma variável \(X\) que padroniza a sua posição (pois a média do z-score é sempre 0, enquanto a média de \(X\) pode ser qualquer coisa) e a sua escala (pois \(X\) pode variar muito ou pouco, com qualquer desvio padrão, mas o z-score não. o z-score terá sempre desvio padrão igual a 1). A fórmula do z-score é:

\[Z_{SCORE} (X) = \frac{X-Média(X)}{Desvio Padrão (X)}\]

Uma estratégia para encontrar outliers, então, é marcar aqueles pontos que, nessa escala, estão muito discrepantes. Normalmente se adota um ponto de corte pequeno, como -2 e 2 ou no máximo -3 e 3. Serão considerados outliers todos os pontos que estiverem fora desse intervalo.

Vamos ver o que aconteceria se usássemos essa regra para arrumar o primeiro gráfico que mostramos? Primeiro, vamos criar uma base de dados onde poderemos trabalhar. Ela se chamará mtcars_com_outliers, como se vê abaixo.

mtcars_com_outliers <- mtcars %>% 
  # aqui vamos incluir os pontos bizarros...
  dplyr::bind_rows(
    tibble::tibble(
      mpg = c(0.1, 1039, 481, 1402),
      wt = c(3.21, 1.8230, 2.6740, 3.6720)
    )
  ) 

Agora, vamos criar uma coluna e_outlier que vai nos dizer se estamos falando de um outlier ou não. Para não perder a viagem, também vamos fazer um gráfico que ajude a identificar visualmente os pontos que podem ser outliers.

mtcars_com_outliers %>% 
  dplyr::mutate(
    z_score_mpg = (mpg-mean(mpg))/sd(mpg),
    e_outlier_mpg = dplyr::if_else(abs(z_score_mpg) > 2, "É outlier", "Não é outlier")
  ) %>% 
  ggplot2::ggplot(ggplot2::aes(x = wt, y = mpg, color = e_outlier_mpg)) +
  ggplot2::geom_point(size = 3) +
  ggplot2::theme_minimal(15) +
  ggplot2::labs(x = "Peso do carro", y = "Consumo de combustível (milhas/galão)", color = "")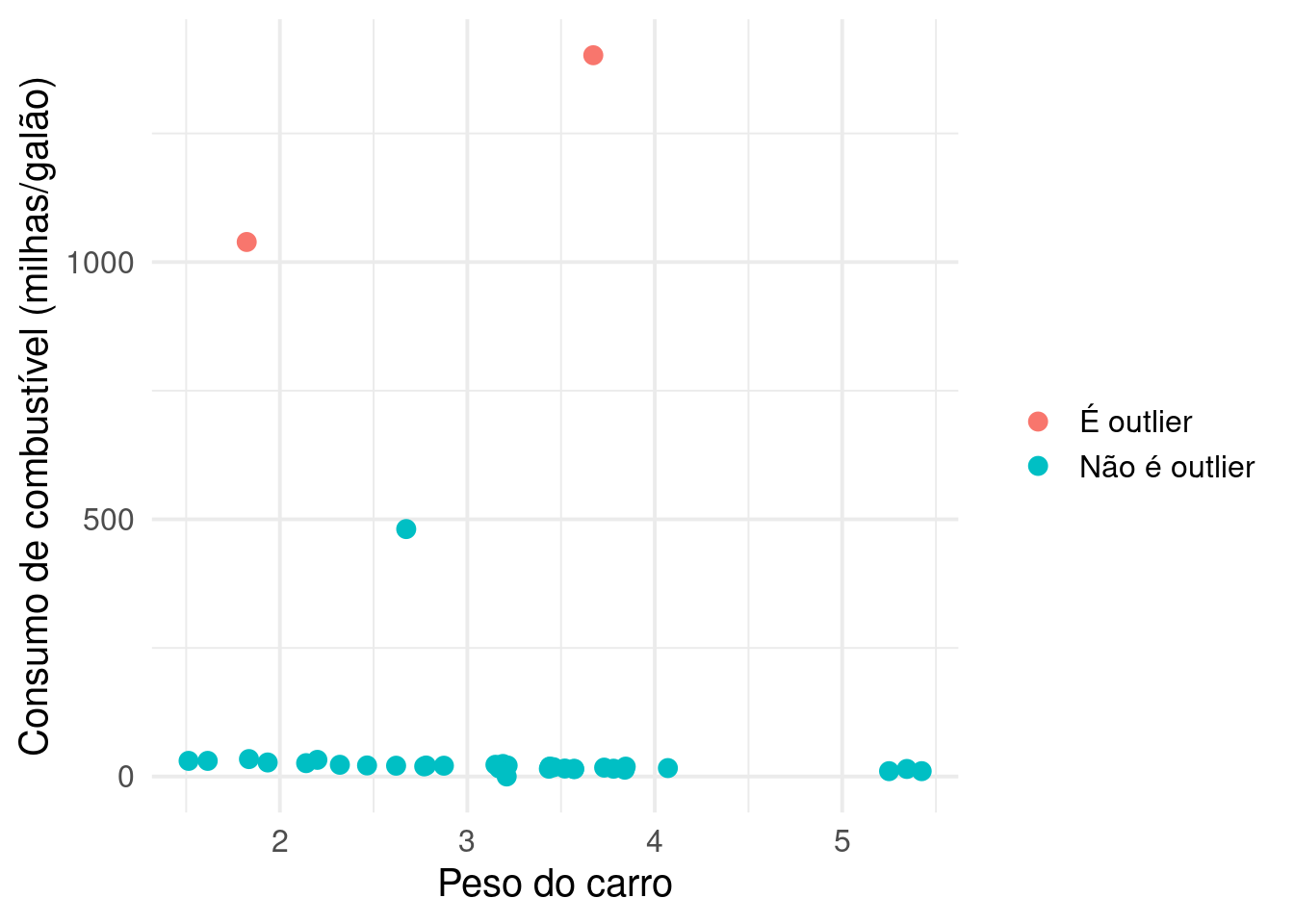

Usamos o ponto de corte 2 e parece que um outlier ficou de fora, né? Vamos diminuir um pouco o ponto de corte e ver se a gente consegue pegar esse que ficou fora.

mtcars_com_outliers %>% 
  dplyr::mutate(
    z_score_mpg = (mpg-mean(mpg))/sd(mpg),
    e_outlier_mpg = dplyr::if_else(abs(z_score_mpg) > 1, "É outlier", "Não é outlier")
  ) %>% 
  ggplot2::ggplot(ggplot2::aes(x = wt, y = mpg, color = e_outlier_mpg)) +
  ggplot2::geom_point(size = 3) +
  ggplot2::theme_minimal(15) +
  ggplot2::labs(x = "Peso do carro", y = "Consumo de combustível (milhas/galão)", color = "")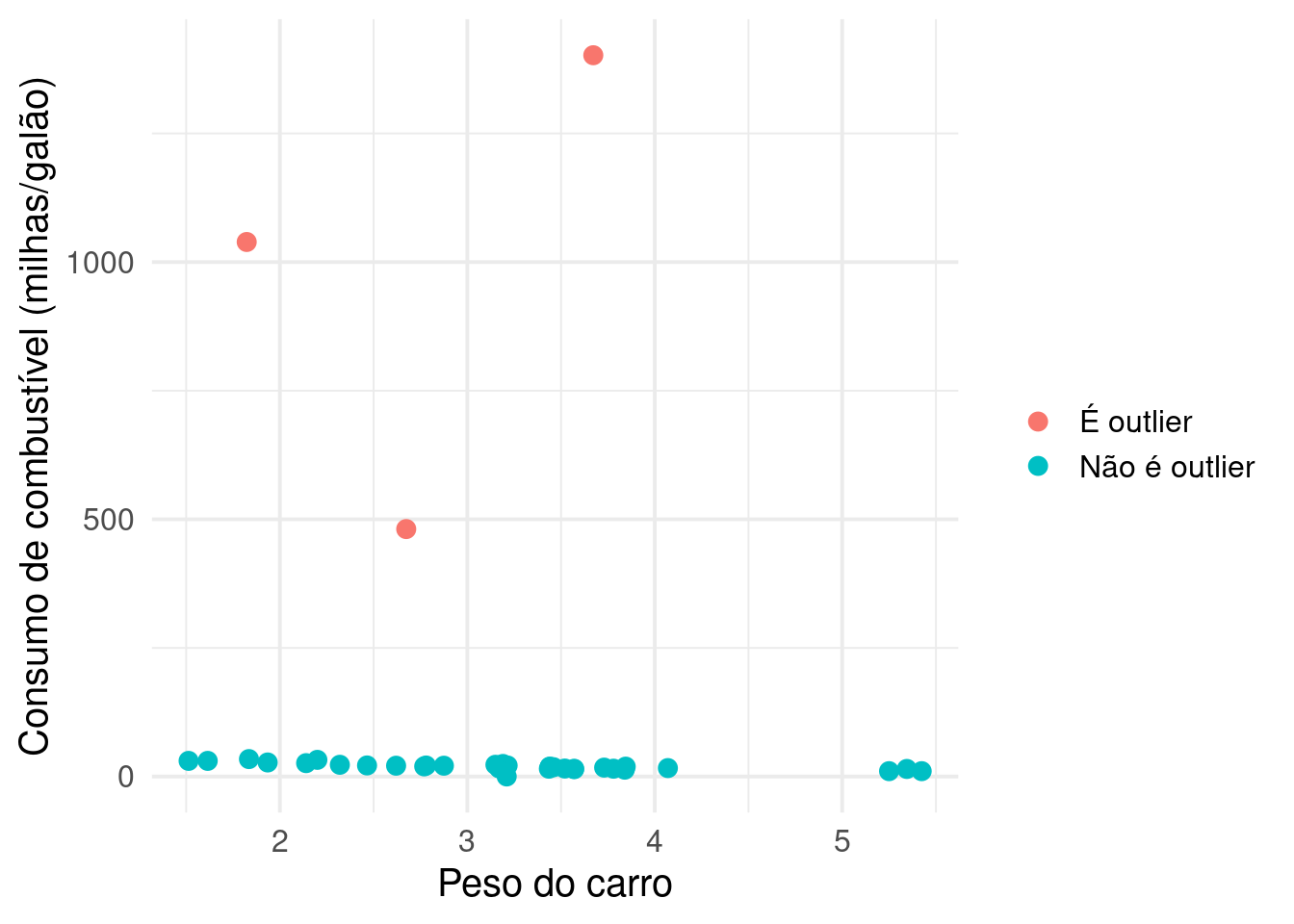

Conseguimos! Vamos fazer um novo plot para analisar os dados do jeito que a gente gostaria de ter feito desde o começo, se não fossem esses outliers chatos.

mtcars_com_outliers %>% 
  dplyr::mutate(
    z_score_mpg = (mpg-mean(mpg))/sd(mpg),
    e_outlier_mpg = dplyr::if_else(abs(z_score_mpg) > 1, "É outlier", "Não é outlier")
  ) %>% 
  dplyr::filter(e_outlier_mpg == "Não é outlier") %>% 
  ggplot2::ggplot(ggplot2::aes(x = wt, y = mpg)) +
  ggplot2::geom_point(size = 3) +
  ggplot2::theme_minimal(15) +
  ggplot2::labs(x = "Peso do carro", y = "Consumo de combustível (milhas/galão)", color = "")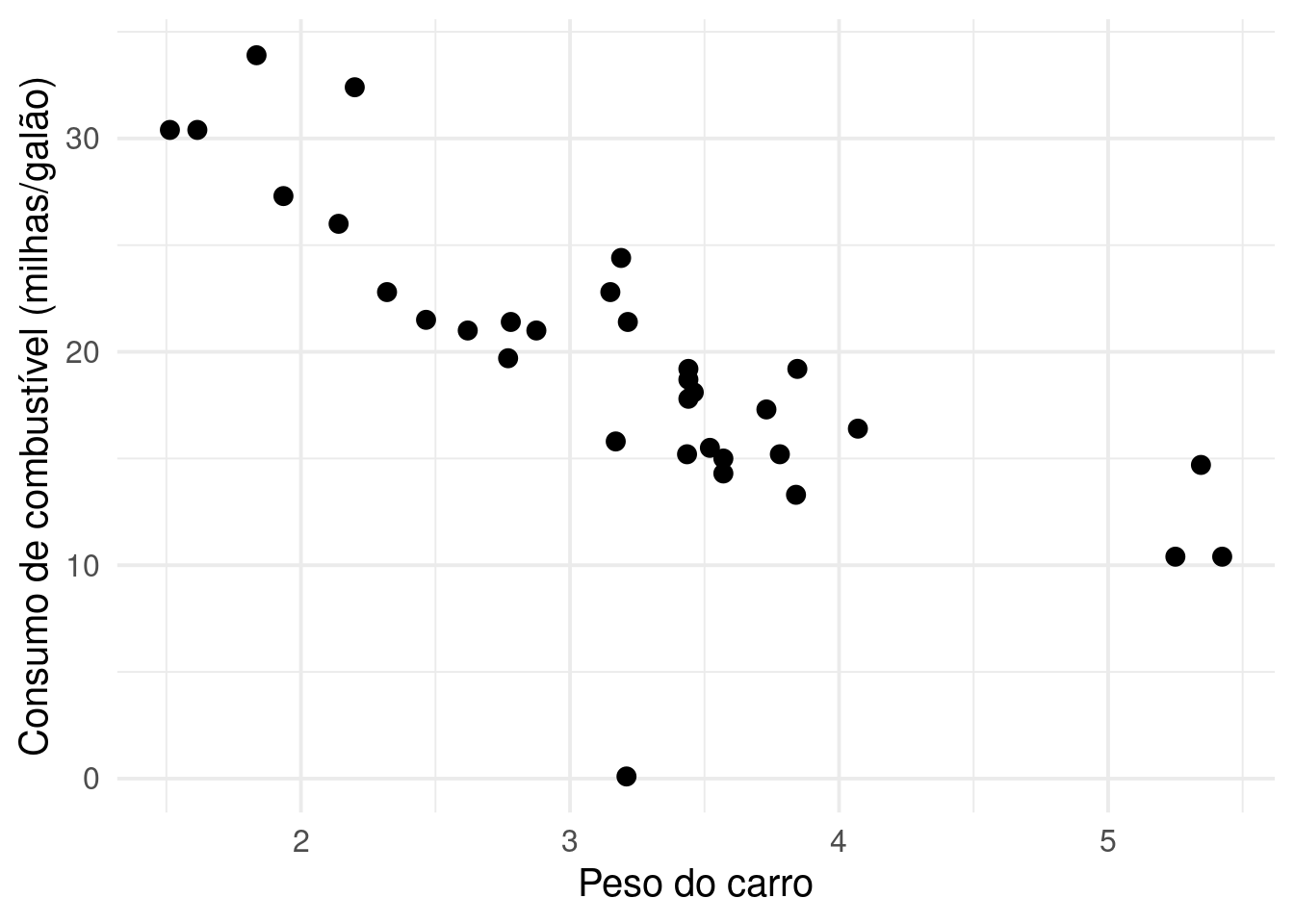

Agora parece que tem mais um, o que é que a gente faz? A gente até poderia repetir o processo: rodar o z-score nessa base filtrada, experimentar alguns cortes, refazer os gráfico e seguir até não conseguirmos identificar nenhum outro outlier. Mas isso não parece escalar muito bem, né?

E se eu te dissesse que tem uma pequena modificação que a gente pode fazer no z-score que simplifica o nosso trabalho? Pois tem, e é o que normalmente se chama de z-score robusto. A fórmula é só um pouquinho diferente:

\[Z_{SCORE}\ ROBUSTO(X) = \frac{X-Mediana(X)}{MAD(X)}\] Se você comparar essa fórmula com a outra que postamos lá em cima, duas coisas mudaram: a média virou mediana e o desvio padrão virou MAD. O MAD é um pouco menos conhecido que a mediana, mas ele está para o desvio padrão assim como a média está para a mediana. Essas duas medidas, o MAD e a mediana, são mais robustas do que a média e o desvio padrão, respectivamente, porque consideram a estatística de ordem central, ao invés de tomar uma média de todos os dados ou, no caso do desvio padrão, uma média de todos os desvio quadráticos. Por conta desse comportamento baseado em estatísticas de ordem, o z-score robusto se comporta muito melhor do que o z-score comum, principalmente quando o assunto é encontrar outliers. De resto, vamos fazer mais ou menos a mesma coisa que fizemos antes: escolher um corte e seguir. Podemos inclusive começar escolhendo 2 ou 3 para ver o que acontece:

mtcars_com_outliers %>% 
  dplyr::mutate(
    z_score_mpg = (mpg-median(mpg))/mad(mpg),
    e_outlier_mpg = dplyr::if_else(abs(z_score_mpg) > 3, "É outlier", "Não é outlier")
  ) %>% 
  ggplot2::ggplot(ggplot2::aes(x = wt, y = mpg, color = e_outlier_mpg)) +
  ggplot2::geom_point(size = 3) +
  ggplot2::theme_minimal(15) +
  ggplot2::labs(x = "Peso do carro", y = "Consumo de combustível (milhas/galão)", color = "")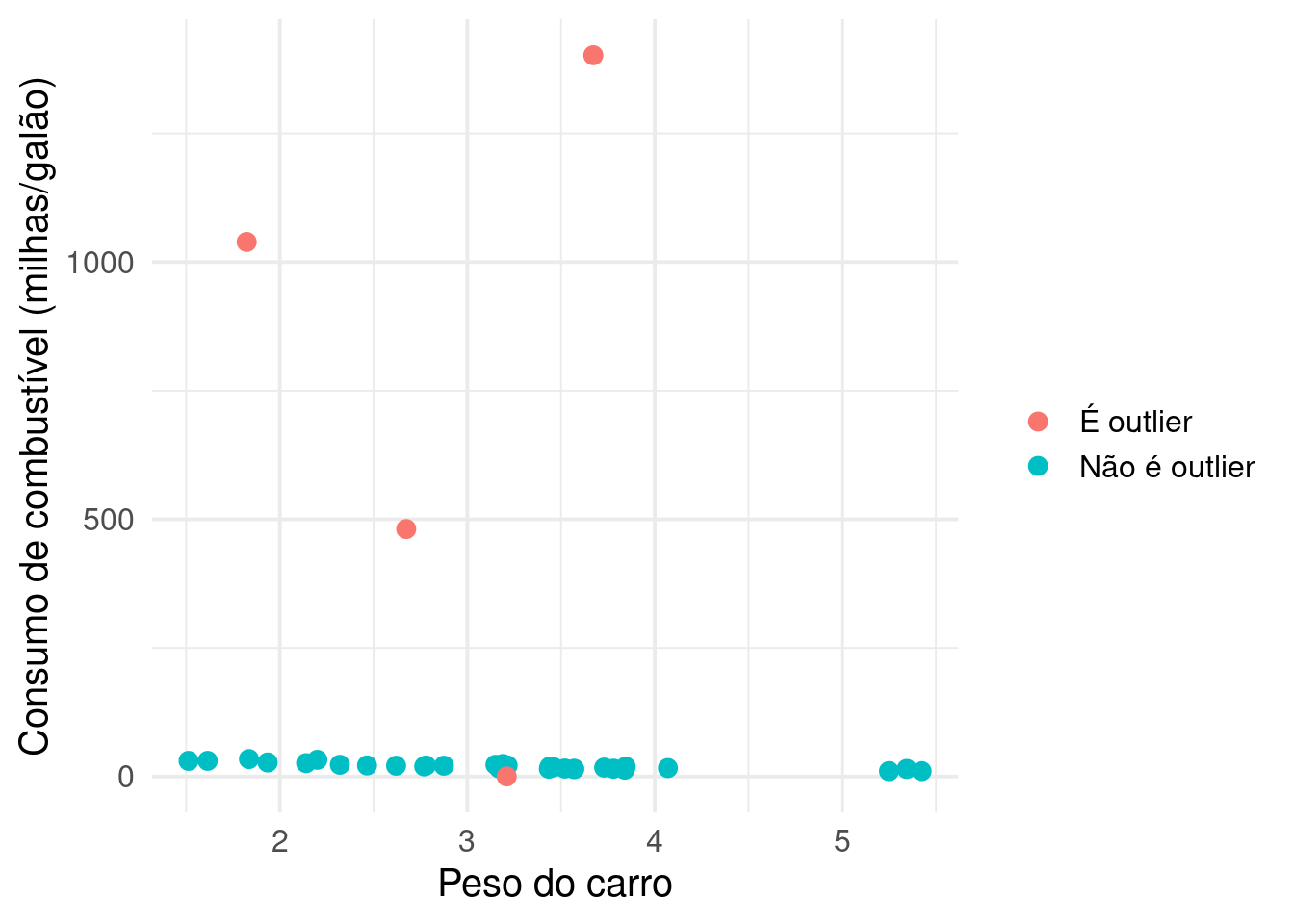

E olha só que beleza, encontramos todos os outliers, sem precisar fazer o próximo gráfico! Legal né?

Conta pra gente aí nos comentários se você já conhecia o z-score robusto e o MAD.