Nesse post vou trabalhar com Captchas e GANs. Se você não sabe o que é um Captcha e como estamos trabalhando para resolvê-los até agora, recomendo que você veja a série de posts da Curso-R sobre o tema. Se você não sabe nada de GAN, acredito que seja possível acompanhar esse post. No entanto, não acho que esse é o exemplo mais simples possível de GAN: se você quiser um “hello world” no tema, recomendo ver esse exemplo e esse paper.
Objetivo: criar um modelo capaz de, ao mesmo tempo, gerar novos Captchas e também resolver Captchas existentes.
Motivo: o motivo principal de usar modelos generativos é aproveitar o fato de existirem muito mais Captchas não classificados do que classificados. De certa forma, saber criar novos Captchas pode auxiliar no trabalho de resolvê-los.
Base de dados: ao invés de utilizar um Captcha real, vamos trabalhar com um Captcha sintético criado partir do MNIST. Chamarei esses carinhas de MNIST-Captcha. A ideia foi simplificar o problema para facilitar o desenvolvimento da solução. Um problema que enfrentamos no Deep Learning é que existem tantos hiperparâmetros a serem escolhidos que é muito difícil achar configurações que funcionam bem. Em problemas mais simples, é mais fácil achar esses parâmetros.
Figura 1: Exemplo de imagem do MNIST.

Figura 2: Exemplo de MNIST-Captcha.
O que é GAN?
A sigla GAN significa Generative Adversarial Networks. Não confunda com GAM (Generalized Additive Models)! Trata-se de um modelo recente, introduzido em 2014 pelo Ian Goodfellow, autor do famoso livro DeepLearningBook, que está ganhando cada vez mais espaço na comunidade científica, por conta de seus impressionantes resultados.
GAN, na verdade, são dois modelos co-dependentes, o gerador e o discriminador. O gerador tenta gerar novos Captchas a partir de nada, indistinguíveis dos originais, e o discriminador tenta discriminar se os Captchas criados pelo gerador são reais ou não. Ou seja, um fica brigando com o outro, e no final temos um excelente gerador de novos Captchas e um excelente discriminador de Captchas.
O que é AC-GAN?
Quando nosso interesse está na predição, simples GANs não ajudam, pois o discriminadores só sabem verificar se uma imagem é original ou fake. No entanto, podemos adicionar respostas no discriminador, tornando-o um modelo duplo, capaz de discriminar imagens reais e falsas e, ao mesmo tempo, capaz de predizer o valor do Captcha.
OK, mas não está claro
Não mesmo. Esses carinhas não são simples. O ideal é sentar na cadeira e tentar entender o que o modelo faz. Eu fiz minha lição de casa, e consegui extrair esses passos:
- Coletar uma amostra das imagens de treino
- Gerar Captchas fake.
- Juntar com Captchas reais.
- Andar 1 iteração no ajuste do discriminador.
- Gerar mais Captchas fake.
- Criar uma variável resposta sintética para avaliar a qualidade do gerador.
- Andar 1 iteração no ajuste do gerador, usando o discriminador para avaliar se as imagens foram bem geradas ou não.
- Voltar ao passo 1 até coletar a totalidade das imagens de treino
- Aplicar os passos 1 até 7 com as imagens de teste, para avaliar a performance dos modelos.
Os passos são até tranquilos de implementar, mas são difíceis de entender. Particularmente, as partes que tive mais dificuldade foram 6 e 7.
Vamos então repassar esses pontos, só que agora assumindo que temos as funções generator() e discriminator() em mãos.
Estrutura do AC-GAN
O generator()
O generator() é uma função que recebe como input i) um vetor de valores aleatórios e ii) uma label de um Captcha, e retorna a imagem de um Captcha. Os valores aleatórios são variáveis latentes que ajudam a criar os ruídos do Captcha: se não fossem eles, todos os Captchas gerados para uma dada label seriam iguais.
Matematicamente, o gerador \(g\) de uma imagem \(i\) se comporta da seguinte forma:
\[ \mathbf X_i = g(\mathbf Y_i, \boldsymbol \varepsilon_i), \]
onde
- \(\mathbf X_i\) é uma imagem. No caso da RFB, uma imagem 50x180.
- \(\mathbf Y_i\) é a label do Captcha, encodada na forma 0-1, como mostrada por esse post
- \(\boldsymbol \varepsilon_i\) é um erro aleatório, usado para que os resultados gerados sejam diferentes toda vez.
- \(g\) é uma função altamente não linear, capaz de receber os inputs mencionados e retornar uma imagem.
Uma forma interessante de representar g() é através de uma rede convolucional ao contrário. Veja os comentários da função para entender o que ela está fazendo.
build_generator <- function() {
# ruído
latent <- layer_input(c(2, 10), name = "noise")
# resposta
label <- layer_input(c(2, 10), name = "sampled_labels")
# obtém o input a partir da soma da resposta e do ruído
input <- layer_add(list(label, latent))
output <- input %>%
# destrói as dimensões existentes e coloca num vetor
layer_flatten() %>%
# remodela as dimensões iniciais da imagem
# aqui, ela fica com 4 "cores" (canais),
# 7 linhas e 14 colunas
layer_dense(4 * 7 * 14, activation = "tanh") %>%
layer_reshape(c(4, 7, 14)) %>%
# A rede convolucional transpose com strides aumenta
# o tamanho da imagem. Agora está em 14 x 28
layer_conv_2d_transpose(64, 3, padding = "same", strides = c(2, 2)) %>%
layer_activation_leaky_relu() %>%
# Agora está em 28 x 56
layer_conv_2d_transpose(64, 3, padding = "same", strides = c(2, 2)) %>%
layer_activation_leaky_relu() %>%
# Agora está em 28 x 112 (note que strides = c(1, 2))
layer_conv_2d_transpose(32, 3, padding = "same", strides = c(1, 2)) %>%
layer_activation_leaky_relu() %>%
# mais algumas convolucionais para gerar não-linearidade
layer_conv_2d(16, 3, padding = "same") %>%
layer_activation_leaky_relu() %>%
layer_conv_2d(16, 3, padding = "same") %>%
layer_activation_leaky_relu() %>%
layer_conv_2d(8, 3, padding = "same") %>%
layer_activation_leaky_relu() %>%
# Reduzir o número de cores para 1 (imagem preto e branco)
layer_conv_2d( 1, 3, padding = "same", activation = "tanh")
# coloca os dois inputs e o output no modelo
keras_model(list(latent, image_class), output)
}
build_generator()Model
___________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
===========================================================================================
noise (InputLayer) (None, 4, 10) 0
___________________________________________________________________________________________
sampled_labels (InputLayer) (None, 4, 10) 0
___________________________________________________________________________________________
add_2 (Add) (None, 4, 10) 0 noise[0][0]
sampled_labels[0][0]
___________________________________________________________________________________________
flatten_4 (Flatten) (None, 40) 0 add_2[0][0]
___________________________________________________________________________________________
dense_10 (Dense) (None, 392) 16072 flatten_4[0][0]
___________________________________________________________________________________________
reshape_5 (Reshape) (None, 4, 7, 14) 0 dense_10[0][0]
___________________________________________________________________________________________
conv2d_transpose_4 (Conv2DTra (None, 64, 14, 28) 2368 reshape_5[0][0]
___________________________________________________________________________________________
leaky_re_lu_10 (LeakyReLU) (None, 64, 14, 28) 0 conv2d_transpose_4[0][0]
___________________________________________________________________________________________
conv2d_transpose_5 (Conv2DTra (None, 64, 28, 56) 36928 leaky_re_lu_10[0][0]
___________________________________________________________________________________________
leaky_re_lu_11 (LeakyReLU) (None, 64, 28, 56) 0 conv2d_transpose_5[0][0]
___________________________________________________________________________________________
conv2d_transpose_6 (Conv2DTra (None, 32, 28, 112) 18464 leaky_re_lu_11[0][0]
___________________________________________________________________________________________
leaky_re_lu_12 (LeakyReLU) (None, 32, 28, 112) 0 conv2d_transpose_6[0][0]
___________________________________________________________________________________________
conv2d_8 (Conv2D) (None, 1, 28, 112) 289 leaky_re_lu_12[0][0]
===========================================================================================
Total params: 74,121
Trainable params: 74,121
Non-trainable params: 0
___________________________________________________________________________________________No caso, nossa resposta é 4747:
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 0 0 0 1 0 0 0 0 0 0
[2,] 0 0 0 0 0 0 1 0 0 0
[3,] 0 0 0 1 0 0 0 0 0 0
[4,] 0 0 0 0 0 0 1 0 0 0E temos uma matriz de números aleatórios do mesmo tamanho:
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] -0.06 0.02 -0.08 0.16 0.03 -0.08 0.05 0.07 0.06 -0.03
[2,] 0.15 0.04 -0.06 -0.22 0.11 0.00 0.00 0.09 0.08 0.06
[3,] 0.09 0.08 0.01 -0.20 0.06 -0.01 -0.02 -0.15 -0.05 0.04
[4,] 0.14 -0.01 0.04 -0.01 -0.14 -0.04 -0.04 -0.01 0.11 0.08Queremos gerar uma resposta com ruído a partir da resposta e de um vetor de números aleatórios. Fazemos isso simplesmente somando as duas quantidades:
round(y + z , 2) [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] -0.06 0.02 -0.08 1.16 0.03 -0.08 0.05 0.07 0.06 -0.03
[2,] 0.15 0.04 -0.06 -0.22 0.11 0.00 1.00 0.09 0.08 0.06
[3,] 0.09 0.08 0.01 0.80 0.06 -0.01 -0.02 -0.15 -0.05 0.04
[4,] 0.14 -0.01 0.04 -0.01 -0.14 -0.04 0.96 -0.01 0.11 0.08Observe que os valores da resposta continuam destacados. O resultado da aplicação do generator() é uma imagem com as mesmas dimensões do MNIST-Captcha e os números dados no input. Queremos que essa imagem seja o mais parecida possível com uma imagem real.
O discriminator()
O discriminador é um modelo preditivo, mas ele prevê duas coisas: i) se a imagem recebida é real ou fake e ii) qual é a label de uma imagem recebida. Se o gerador for bom, (i) terá dificuldades para funcionar. Se o gerador for muito ruim (i) conseguirá prever resultados com facilidade.
Vamos a um exemplo de discriminador, também usando redes convolucionais:
build_discriminator <- function() {
image <- layer_input(shape = c(1, 28, 28*4))
# rede convolucional LENET-5 bem comum
output <- image %>%
layer_conv_2d(32, 5, padding = "same") %>%
layer_activation_leaky_relu() %>%
layer_max_pooling_2d() %>%
layer_conv_2d(64, 5, padding = "same") %>%
layer_activation_leaky_relu() %>%
layer_max_pooling_2d() %>%
layer_conv_2d(64, 3, padding = "same") %>%
layer_activation_leaky_relu() %>%
layer_flatten() %>%
layer_dense(64, activation = "relu") %>%
layer_dropout(0.2) %>%
layer_dense(128, activation = "relu")
cnn <- keras_model(image, output)
features <- cnn(image)
# chega a primeira resposta (fake, não fake)
fake <- features %>%
layer_dense(32, activation = "tanh") %>%
layer_dense(1, activation = "sigmoid", name = "generation")
# chega na segunda resposta (Y)
aux <- features %>%
layer_dense(4 * 10, activation = "relu") %>%
layer_reshape(c(4, 10)) %>%
layer_activation("softmax", name = "auxiliary")
# junta os dois no resultado
keras_model(image, list(fake, aux))
}
build_discriminator()Model
___________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
===========================================================================================
input_4 (InputLayer) (None, 1, 28, 112) 0
___________________________________________________________________________________________
model_5 (Model) (None, 128) 900224 input_4[0][0]
___________________________________________________________________________________________
dense_9 (Dense) (None, 40) 5160 model_5[1][0]
___________________________________________________________________________________________
dense_8 (Dense) (None, 32) 4128 model_5[1][0]
___________________________________________________________________________________________
reshape_4 (Reshape) (None, 4, 10) 0 dense_9[0][0]
___________________________________________________________________________________________
generation (Dense) (None, 1) 33 dense_8[0][0]
___________________________________________________________________________________________
auxiliary (Activation) (None, 4, 10) 0 reshape_4[0][0]
===========================================================================================
Total params: 1,819,090
Trainable params: 909,545
Non-trainable params: 909,545
___________________________________________________________________________________________Note que o resultado é uma lista de dois outputs.
O gan()
gan() é a função que junta o discriminador e o gerador. Em teoria, ela não serve para nada: é só um meio prático de ajustar o modelo do gerador. Fazemos isso gerando algumas imagens falsas e avaliando a qualidade do gerador por quanto ele é capaz de enganar o discriminador. Se o discriminador é muito ruim, qualquer gerador vai mandar bem. Se o discriminador é muito bom, o gerador terá de criar Captchas excepcionais para ganhar pontos.
O gan() é definido de forma muito simples, com:
# placeholder para ruído
latent <- layer_input(shape = list(4L, 10L))
# placeholder para resposta
image_class <- layer_input(shape = list(4L, 10L))
# imagem falsa
fake <- generator(list(latent, image_class))
# Only want to be able to train generation for the combined model
# Só queremos treinar o generator nessa parte;
# utilizaremos o discriminator apenas para
# avaliação da qualidade do gerador.
# Por isso, congelamos o discriminator aqui.
freeze_weights(discriminator)
results <- discriminator(fake)
gan <- keras_model(list(latent, image_class), results)
ganModel
___________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
===========================================================================================
input_5 (InputLayer) (None, 4, 10) 0
___________________________________________________________________________________________
input_6 (InputLayer) (None, 4, 10) 0
___________________________________________________________________________________________
model_7 (Model) (None, 1, 28, 112) 74121 input_5[0][0]
input_6[0][0]
___________________________________________________________________________________________
model_6 (Model) [(None, 1), (None, 909545 model_7[1][0]
===========================================================================================
Total params: 983,666
Trainable params: 74,121
Non-trainable params: 909,545
___________________________________________________________________________________________Mas funciona?
É uma pergunta natural. Esse modelo é meio maluco, pois usa uma parte do modelo para avaliar a qualidade do outro. Mas sim, temos alguns resultados matemáticos que garantem que estamos em um bom território.
Meu desejo era colocá-los aqui, mas ainda não sei explicar todos os detalhes. Pretendo estudar mais e adicionar em novos posts.
Exemplo de aplicação nos MNIST-Captcha
O exemplo completo que rodei com os MNIST-Captchas está neste link. Decidi não colocar o código completo aqui pois a minha implementação está muito feia o post ficaria muito longo.
Muito bem, se o modelo serve para prever e para gerar, vamos avaliar a qualidade nesses quesitos.
Prevê bem?
A taxa de acerto de cada dígito do MNIST-Captcha foi de 95%. Como temos 4 dígitos nesse caso, o acerto de todo o Captcha seria de 81%. Comparado com os modelos funcionando em produção do pacote decryptr, esse resultado é ruim. Lá, as taxas de acerto do Captcha são de no mínimo 93% e tem casos que acertamos tudo. Mas eu acredito que o motivo disso é que não ajustamos bem os hiperparâmetros. Se fizermos isso, provavelmente ficará melhor.
Gera bem?
Vamos ver! Para testar o gerador, montamos uma função que gera e plota uma imagem a partir de um vetor de respostas:
generate_image <- function(num = sample(0:9, 4)) {
# Gerando barulho
noise <- rnorm(4 * 10, 0, .01) %>%
array(dim = c(4, 10)) %>%
array_reshape(c(1, dim(.)))
# Resposta (aleatorizada ou input)
sampled_labels <- num %>%
matrix(ncol = 4) %>%
# gera o one-hot dessa resposta
transform_to_matrix() %>%
array_reshape(c(1, dim(.)))
# Aplicar generator
img <- predict(generator, list(noise, sampled_labels))[1,1,,]
# a imagem foi deixada em (-1,1). Arrumando
par(mar = rep(0, 4))
plot(as.raster((img + 1) / 2))
}Rodando para alguns exemplos:
gerar_imagem(c(1, 2, 4, 4))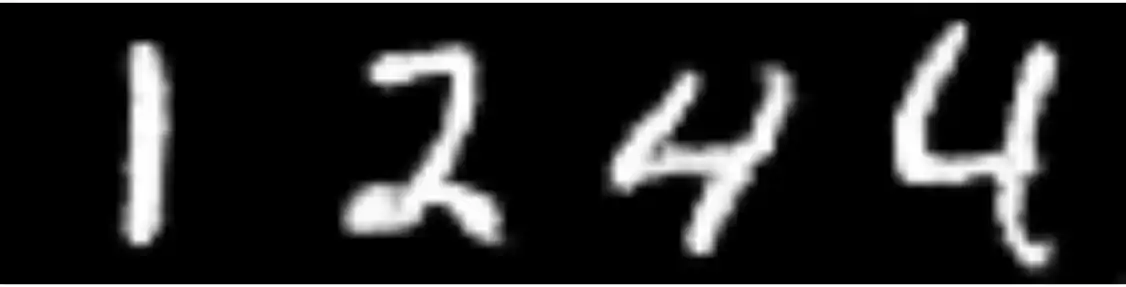
gerar_imagem(c(4, 0, 4, 7))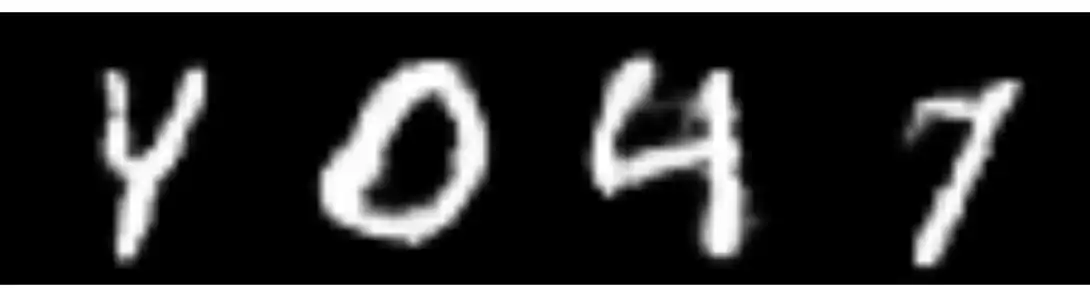
gerar_imagem(c(9, 9, 9, 9))
O que achou? Note que a última está errada.
Próximos passos
- Fazer o GAN funcionar para mais Captchas.
- Testar algumas dicas que o Athos me passou.
- Buscar uma forma de aproveitar a informação parcial advinda de oráculos. Fica o mistério para os próximos posts.
Wrap-up
- GAN é um modelo interessante que pode nos ajudar a montar modelos não supervisionados (diretamente) e supervisionados (AC-GAN).
- Para montar um GAN, você precisa definir um gerador e um discriminador.
- O AC-GAN parece ser uma boa abordagem para Captchas, considerando que temos muitas imagens disponíveis e poucas classificadas.
- Ainda temos muito a descobrir sobre esse modelo.
Agradecimentos
Sempre ao Daniel Falbel, que é meu guru do Deep Learning e autor do exemplo inicial que foi adaptado para esse post. Também agradeço ao Athos pelos insights e links que me passou!


