Esse post serve como introdução aos modelos de suavização exponencial e replica
um exemplo disponível no livro Forecasting principles and practice (FPP)
disponível aqui. Em seguida implementamos usando o
pacote rstan uma abordagem bayesiana
para o mesmo problema usando como referência o paper Fitting and Extending Exponential Smoothing Models with Stan.
Vamos portanto começar descrevendo o modelo de suavização exponencial simples.
Fazer um exemplo inicial usando o conhecido pacote forecast e partir para a implementação
com rstan.
Suavização exponencial simples
Suavização exponencial é uma das principais classes de modelos usados em previsão de séries temporais. Essa classe inclui diversos tipos de modelos como o bem conhecido Holt Winters e até o Theta Method - conhecido por ter ido bem em uma M3-competition.
A suavização exponencial simples, com o próprio nome diz, é o caso particular mais simples de suavização exponencial. Esse tipo de modelo serve para quando não existe nenhum padrão claro de sazonalidade ou tendência na série.
Nesta parte introdutória vou parafrasear o próprio Hyndman no FPP.
Considere que \(y_t\) seja a observação no tempo t de uma série temporal. O modelo mais simples
possível e que também é chamado de ingênuo (naive) seria:
\[y_{T+1|T} = y_{T}\] Isto é, a previsão para \(T+1\) dado que conhecemos o valor da série até o instante \(T\) seria simplesmente o último valor observado da série \(y_T\). Neste modelo, a última observação da série é única importante para prever o seu próximo valor.
Agora considere um modelo chamado Average method em que consideraremos que a previsão para a próxima observação da série é a média aritmética de todos os valores anteriores da série. Em notação matemática:
\[y_{T+1|T} = \frac{1}{T}\sum_{t=1}^{T}y_t\]
Neste modelo, todas as observações anteriores da série possuem o mesmo peso (\(1/T\)) na previsão do próximo valor da série.
Em geral queremos um meio termo. Não queremos que todas as observações tenham o mesmo peso, nem que só a última tenha o maior peso. Poderíamos escrever um modelo assim:
\[y_{T+1|T} = \sum_{t=1}^{T}\beta_t*y_t\] Com \(\sum_{t=1}^{T}\beta_t = 1\). Neste modelo cada observação do passado teria um pesinho \(\beta_t\) que poderíamos estimar por meio de algum algoritmo. A previsão para o próximo período da série seria uma média ponderada das observações passadas.
No entanto, isso não é viável pois teríamos tantos parâmetros quanto observações.
Para simplificar esse problema, a suavização exponencial faz a suposição de que o peso das observações passadas vai diminuindo conforme elas estão mais distantes do ponto que estamos tentando prever. Mais especificamente esses pesos decaem exponencialmente com o passar do tempo. Portanto, o modelo é reescrito para:
\[y_{T+1|T} = \alpha y_t + \alpha(1 - \alpha)y_{t-1} + \alpha(1 - \alpha)^2y_{t-2} + ...\]
Em que \(0 \le \alpha \le 1\) é o parâmetro de suavização. Neste modelo a previsão para o próximo período da série é uma média ponderada das observações passadas em que os pesos decrescem exponencialmente com uma taxa \(\alpha\).
Quando \(\alpha \approx 0\) então as observações mais distantes damos mais peso para as observações mais distantes. Quando \(\alpha = 1\) ficamos exatamente com o modelo ingênuo.
A forma de componentes
Em suavização exponencial é comum escrever os modelos em forma de componentes. Isso facilita extensões como adicionar tendências e sazonalidades. Para fazer suavização exponencial simples só precisamos do componente \(l_t\) (de level). Em outros métodos também usam-se os componentes \(b_t\) (tendência) e \(s_t\) (sazonalidade).
Na forma de componente escrevemos o modelo da seguinte forma:
- Equação de previsão: \(\hat{y_{t+1|t}} = l_t\).
- Equação de suavização: \(l_t = \alpha y_t + (1 - \alpha )l_{t-1}\)
Note que essa forma é equivalente ao que escrevemos anteriormente - basta substituir \(l_t\) por \(\hat{y_{t+1|t}}\) e \(l_{t-1}\) por \(\hat{y_{t|t-1}}\) na equação de suavização.
Escrevendo o modelo desta forma fica fácil de ver que precisamos escolher dois parâmetros: \(\alpha\) e \(l_0\). Com os dois conseguimos prever qualquer valor da série.
Antigamente (antes de computadores existirem) era comum definir \(l_0\) como o primeiro valor observado da série e \(\alpha\) uma valor pequeno, por exemplo \(0,2\).
Hoje em dia temos jeitos melhores de encontrar bons valores para \(\alpha\) e \(l_0\).
Podemos minimizar a soma dos quadrados dos resíduos:
\[SSE = \sum_{t=1}^{T}(y_t - \hat{y}_{t|t-1})^2\]
Ou assumir que \(y_t \sim Normal(l_t, \sigma^2)\) e estimar via máxima verossimilhança.
É isso que a função ses do pacote forecast faz. As contas da verossimilhança são
chatinhas, mas dá para provar que para suavização exponencial simples as duas abordagens
são equivalentes.
Como não é possível resolver algébricamente o problema de minimização, precisamos de
um algoritmo numérico. A função ses também possui algumas heurísticas para decidir
os valores iniciais dos parâmetros.
Tudo isso está escrito no livro Forecasting with Exponential Smoothing também do Hyndman et al.
Exemplo
No exemplo, vamos usar esse banco de dados oil que vem no pacote fpp (do livro FPP).
Esse banco de dados contém a produção anual de petróleo na Arábia Saudita.
Para o exemplo pegamos dados desde 1996 até 2010.
library(forecast)
## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo
library(fpp)
## Loading required package: fma
## Loading required package: expsmooth
## Loading required package: lmtest
## Loading required package: zoo
##
## Attaching package: 'zoo'
## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numeric
## Loading required package: tseries
data(oil)
oildata <- window(oil, start=1996)
plot(oildata)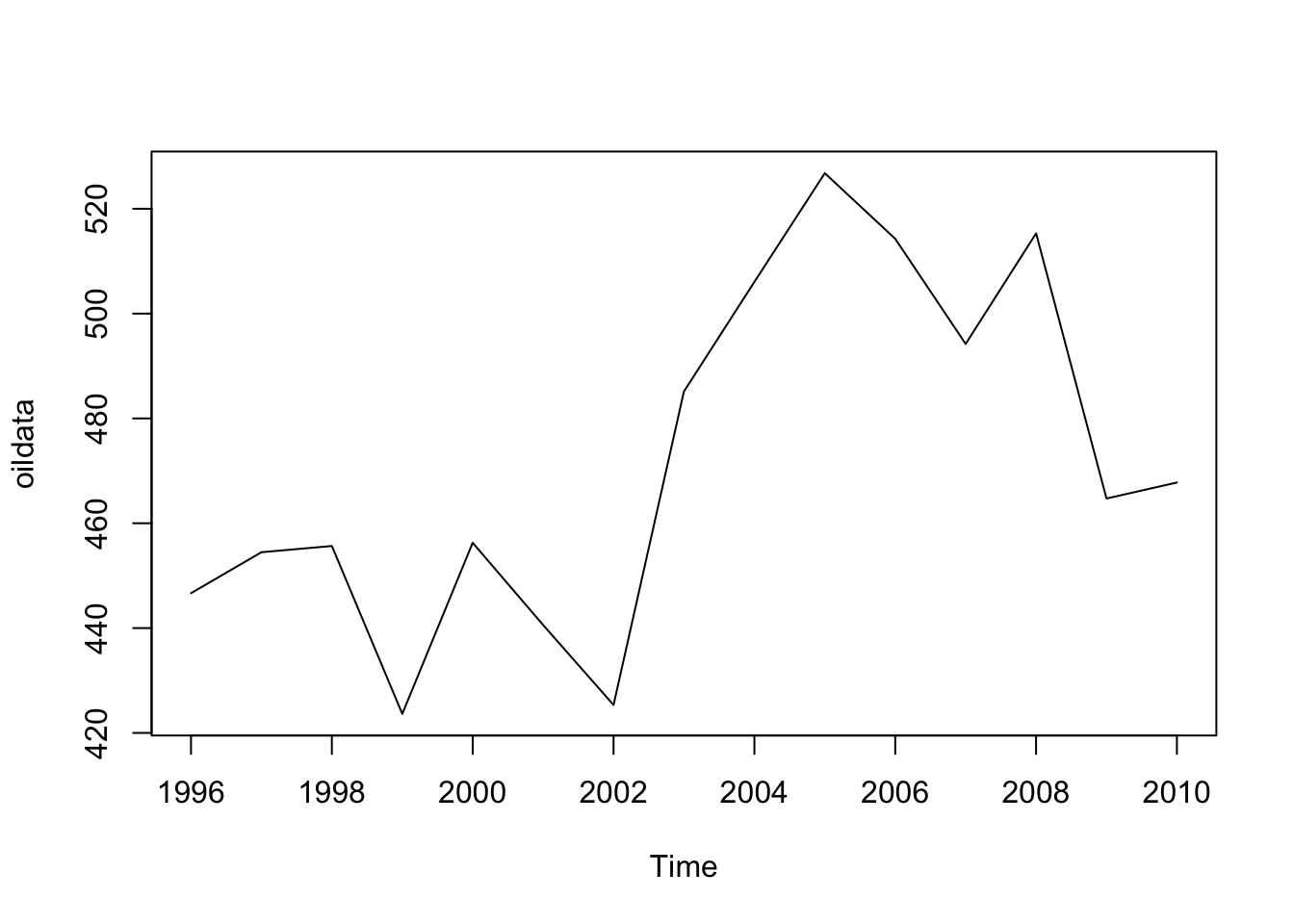
Para ajustar um modelo de suavização exponencial simples com o forecast podemos usar a função
ses, mas ela já retorna os valores preditos para os próximos anos e não nos dá a oportunidade
de ver os valores de \(\alpha\) e \(l_0\) que ela escolheu.
ses(oildata)
## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## 2011 469.2669 433.4186 505.1153 414.4416 524.0923
## 2012 469.2669 423.6608 514.8730 399.5184 539.0155
## 2013 469.2669 415.6505 522.8834 387.2676 551.2663
## 2014 469.2669 408.6902 529.8437 376.6228 561.9110
## 2015 469.2669 402.4512 536.0827 367.0810 571.4529
## 2016 469.2669 396.7469 541.7870 358.3571 580.1768
## 2017 469.2669 391.4597 547.0742 350.2710 588.2629
## 2018 469.2669 386.5096 552.0243 342.7005 595.8334
## 2019 469.2669 381.8393 556.6946 335.5579 602.9760
## 2020 469.2669 377.4061 561.1277 328.7780 609.7559Na nomenclatura do Hyndman para os modelos da classe de suavização exponencial, a suavização exponencial simples é chamada de ANN. Não vou entrar em detalhes mas, isto está descrito aqui.
Usamos então a função ets com o argumento model = "ANN".
modelo <- ets(oildata, "ANN")
modelo
## ETS(A,N,N)
##
## Call:
## ets(y = oildata, model = "ANN")
##
## Smoothing parameters:
## alpha = 0.7869
##
## Initial states:
## l = 448.1262
##
## sigma: 27.9726
##
## AIC AICc BIC
## 144.4110 146.5929 146.5352Agora sim, podemos ver os valores estimados para \(\alpha\) e \(l_0\).
plot(forecast(modelo, h=5))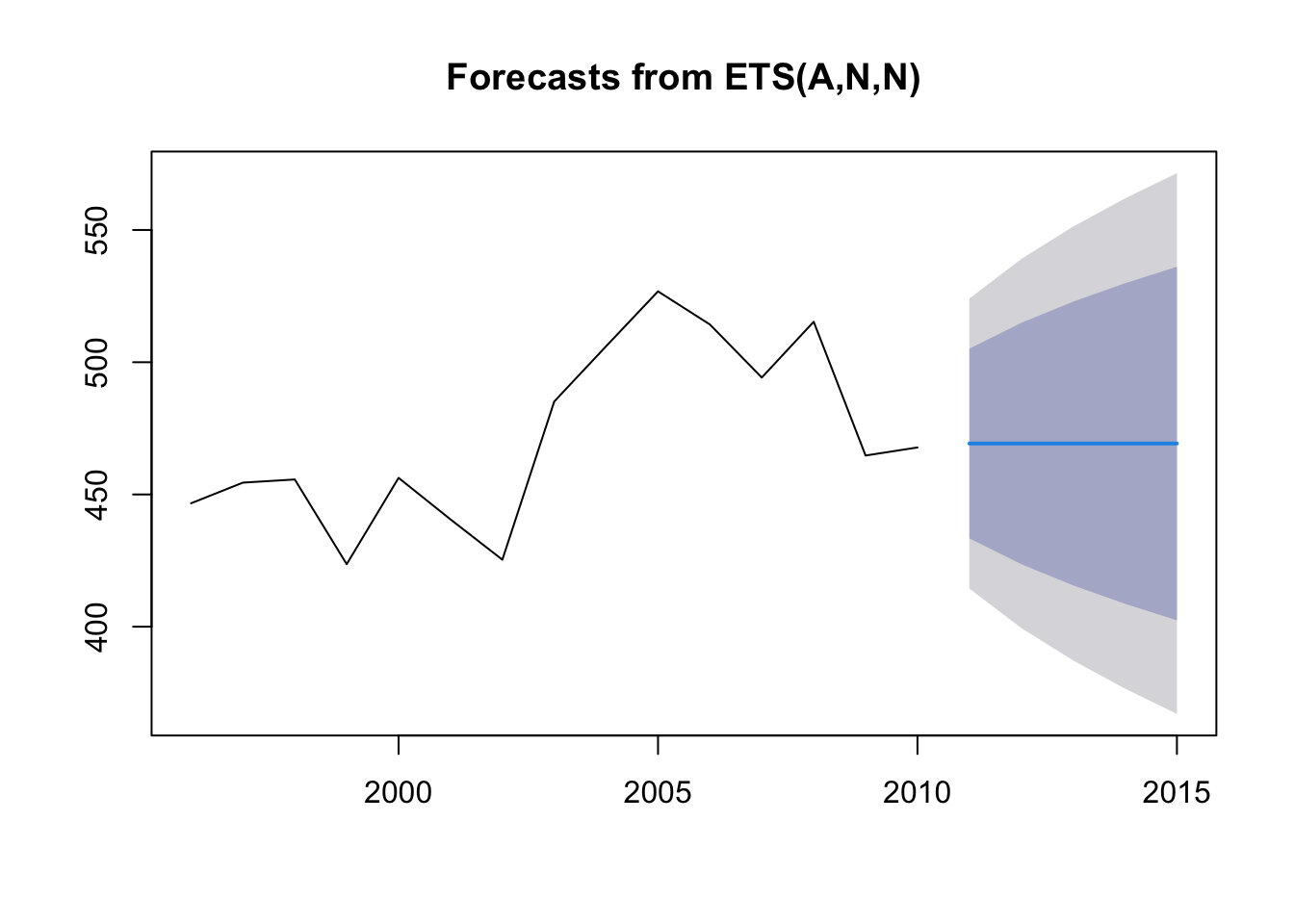
Até aqui vimos como funciona o método de suavização exponencial simples, como o pacote
forecast estima os seus parâmetros (método de máxima verossimilhança) e como fazer
para ajustar esse modelo com o forecast, bem como obter os valores estimados para
os parâmteros.
Agora vamos tentar obter estimativas para os parâmetros \(\alpha\) e \(l_0\) usando uma abordagem bayesiana.
A abordagem bayesiana
A partir do momento que sabemos escrever o modelo e sabemos todos os parâmetros que precisamos estimar fica fácil fazer com Stan.
Para quem não conhece, Stan é uma plataforma para ajustar modelos probabilísticos e possui uma linguagem probabilística própria. Quando você escreve os modelos nessa linguagem, o Stan consegue compilar o seu modelo e criar um programa em C++ muito rápido para ajustar o seu modelo.
Abaixo definimos o modelo de suavização exponencial simples usando a linguagem probabilística do Stan. Esse código é uma leve adaptação do código que está neste paper do Slawek Smyl (esse cara é muito bom, trabalha na Uber e ganhou recentemente competições de forecast).
Veja que na linguagem definimos quais são os dados de entrada:
- n - o tamanho da série
- y - um vetor de tamanho
ncom valores positivos. - mean_y - a média dos valores de
y - var_y - a variância dos valores de
y
Em seguida define quais são os parâmetros:
- sigma - variância do erro
- alpha - parâmetro da suavização exponencial
- l_0 - valor inicial do componente nível.
Em seguida define os parâmteros transformados - aqueles que podem ser obtidos
a partir dos valores definidos em parameters.
Por fim, definimos o modelo.
- Primeiro dizemos que a priori do sigma é a cauda positiva de uma cauchy.
- Depois que a priori para \(l_0\) é uma Normal com a mesma média e desvio padrão do que a própria série.
- Falamos que \(y_t\) tem distribuição normal com média \(l_{t-1}\) e desvio padrão \(sigma\).
- Não especificar uma priori para \(\alpha\) indica que estamos assumindo uma priori uniforme no intervalo.
data {
int<lower=1> n;
vector<lower=0>[n] y;
real<lower=0> mean_y;
real<lower=0> sd_y;
}
parameters {
real<lower=0> sigma;
real <lower=0,upper=1>alpha;
real l_0;
}
transformed parameters {
vector<lower=0>[n] l;
l[1] = l_0;
for (t in 2:n) {
l[t] = alpha*y[t] + (1-alpha)*(l[t-1]) ;
}
}
model {
sigma ~ cauchy(0,2) T[0,]; // positive side of Cauchy distribution as prior
l_0 ~ normal(mean_y, sd_y);
for (t in 2:n) {
y[t] ~ normal(l[t-1], sigma);
}
}Agora ajustamos o modelo e obtemos as estimativas dos parâmetros.
library(rstan)
data <- list(
n = length(oildata),
y = as.numeric(oildata),
mean_y = mean(oildata),
sd_y = sd(oildata)
)
model <- sampling(ann, data = data)print(model, pars = c("sigma", "l_0", "alpha"))
## Inference for Stan model: 7201dbd28b82b04c1f1a89c8607dc886.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
##
## mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
## sigma 28.72 0.10 5.87 19.78 24.70 27.79 31.85 42.15 3184 1
## l_0 460.02 0.36 20.76 419.79 446.52 459.43 473.98 501.41 3260 1
## alpha 0.71 0.00 0.19 0.25 0.59 0.74 0.86 0.98 3852 1
##
## Samples were drawn using NUTS(diag_e) at Mon Jan 25 20:11:49 2021.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).Pelo menos o Stan já nos dá a previsão para 2011 por meio do parâmetro l_15:
print(model, par = "l[15]")
## Inference for Stan model: 7201dbd28b82b04c1f1a89c8607dc886.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
##
## mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
## l[15] 471.88 0.07 4.46 467.73 468.31 470.13 474.18 483.14 4029 1
##
## Samples were drawn using NUTS(diag_e) at Mon Jan 25 20:11:49 2021.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).Sabemos que é o l[15] pois sabemos que \(y_{T+1|T} = l_t\) e \(T=15\) na nossa série.
Bom, como era de se esperar, as estimativas dos parâmetros ficaram parecidas com
as do pacote forecast. Então por que usar Stan? No forecast ele já me dá a previsão
com intervalo de confiança - aqui vou ter que escrever tudo do zero.
A vatangem é flexibilidade. O paper do Slawek comenta bastante sobre isso:
First, the variations among consecutive time series points are sometimes too large to be fully captured by a light-tailed distribution like the Normal Distribution. Second, the time series sometimes have growth rates faster than linear but slower than exponential. Third, the randomness of the time series often grows with values. Fourth, from the business side, expert subjective information should be integrated into forecasting. Last but not least, from the implementation side, forecasts should be generated in a scalable and automated fashion when hundreds or even thousands curves to be forecasted every day. The forecasting methodology should require a minimum amount of data scientists’ attention when in production mode.
Escrevendo o modelo probabilístico com Stan, podemos lidar com cada um desses pontos para definir um modelo mais adequado.
Conclusão
Aprendemos:
- O que são e como funcionam os modelos de suavização exponencial simples.
- Como ajustá-los com o pacote
forecaste como oforecastajusta esses modelos. - Como ajustar SES no Stan.


