Estou bem longe de ter experiência em modelagem bayesiana usando linguagens de
programação probabilística como Stan ou BUGS, mas vi esse pacote chamado greta
que me chamou a atenção.
O greta é um pacote feito totalmente em R, mas que usa o TensorFlow como backend
para fazer os seus cálculos. Isso tudo por intermédio do reticulate. A vantagem de
usar o TensorFlow como backend é a escalabilidade: o greta pode ser rápido até
mesmo em bases de dados grandes e também pode ser acelerada usando clusters de CPU’s
ou GPU’s.
O greta já está disponível no CRAN e pode ser instalado com:
install.packages("greta")Vou mostrar um exemplo simples copiado da página de início do site do próprio
greta e depois vou implementar um modelo que o Fernando implementou aqui no blog
em um outro post sobre estimar um modelo heterocedástico no R.
Exemplo simples
Vamos implementar o modelo de regressão linear mais simples possível. Temos duas variáveis contínuas \(x\) e \(y\) e queremos estimar um modelo da forma:
\[y = a + b*x + \epsilon\]
em que \(\epsilon\) possui distribuição normal com média zero e desvio padrão \(\sigma\). No greta isso pode ser feito da seguinte forma:
library(greta)
# define as variáveis x e y
x <- iris$Petal.Length
y <- iris$Sepal.Length
# define a distribuição priori dos parâmetros
a = normal(0, 5)
b = normal(0, 3)
sd = lognormal(0, 3)
# define o modelo
mean <- a + b * x
distribution(y) = normal(mean, sd)
m <- model(a, b, sd)
# retira amostras usando mcmc
draws <- mcmc(m, n_samples = 1000)Você pode fazer um gráfico para visualizar as estimativas dos parâmetros usando o
bayesplot:
bayesplot::mcmc_trace(draws, facet_args = list(ncol = 1))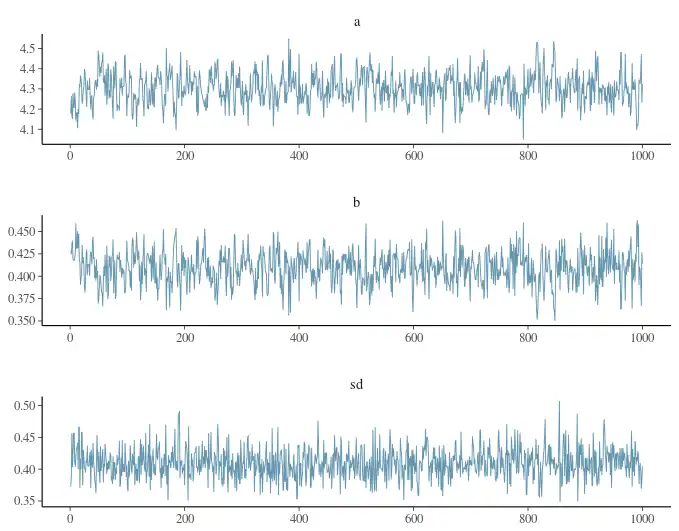
Podemos obter as estimativas pontuais dos parâmetros pegando, por exemplo, a mediana dessa amostra do MCMC.
apply(draws[[1]], 2, median)
## a b sd
## 4.2805710 0.4219092 0.3697692Esse resultado é muito similar ao que pode ser obtido por uma regressão linear simples:
lm(y ~ x)
##
## Call:
## lm(formula = y ~ x)
##
## Coefficients:
## (Intercept) x
## 4.3066 0.4089Modelo linear heterocedástico
Neste post
o Fernando simulou um banco de dados que é heterocedástico e depois ajustou um modelo
deste tipo de diversas maneiras, vou acrescentar mais uma aqui, desta vez usando o greta.
Vou simular o banco de dados da mesma forma que o Fernando:
library(ggplot2)
N <- 1000
set.seed(11071995)
X <- sample((N/100):(N*3), N)
Y <- rnorm(N,X,4*sqrt(X))
qplot(X,Y) +
theme_bw(15) +
geom_point(color = 'darkorange')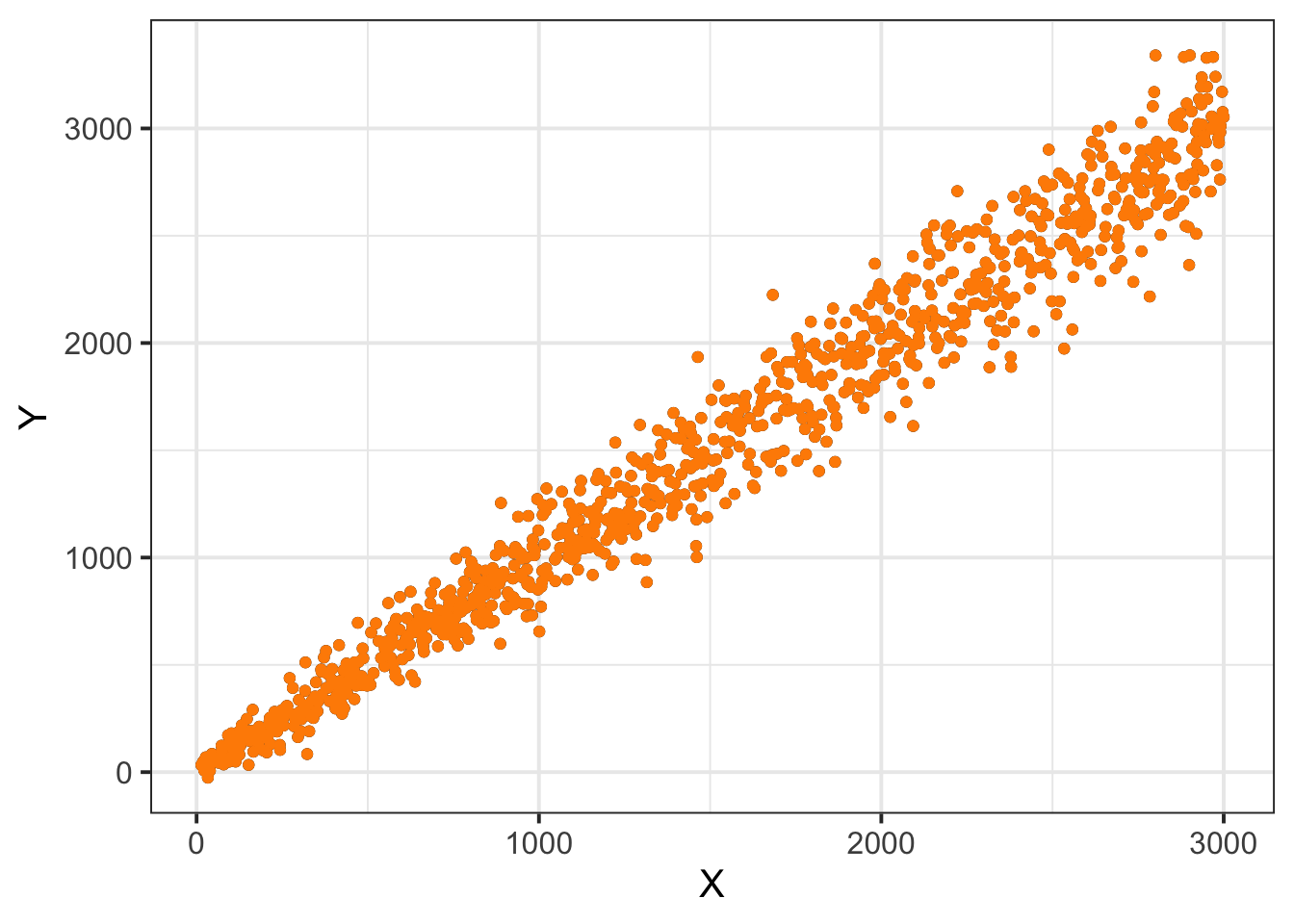
X2 <- sqrt(X)
dataset <- data.frame(Y,X,X2)Agora o código em greta para ajustar esse modelo:
# definir os vetores
y <- dataset$Y
x <- dataset$X
x2 <- dataset$X2
# definir prioris dos parâmetros
alpha <- gamma(1, 1)
beta <- normal(0, 10)
# definir ligações
mean <- beta * x
sd <- alpha * x2
# definir o modelo
distribution(y) = normal(mean, sd)
m <- model(alpha, beta)
# ajustar
draws <- mcmc(m, n_samples = 1000)Agora as estimativas pontuais:
apply(draws[[1]], 2, median)
## alpha beta
## 4.077689 1.002791Como esperado, chegamos em estimativas bem próximas do que foi simulado.
Por hoje é isso!! Abraços!


