São Paulo é a minha cidade preferida. Não só porque moro aqui, mas também porque é uma cidade cheia de diversidade, boa gastronomia e oportunidades. Para sentir um pouco dessa vibe, recomendo passear na avenida Paulista aos domingos. É sensacional!
Mas a cidade da diversidade só é o que é porque temos muita, muita gente nela. O município tem 12 milhões de habitantes. Esse número é tão grande que temos um paulistano para cada 17 brasileiros! Se São Paulo fosse um país, seria o 77 do mundo, ganhando de países como a Bélgica, Grécia, Portugal, Bolívia e muitas outras.
Outro dia eu estava pensando na seguinte problemática: qual é a área do Brasil ocupada pela população de São Paulo? Ou seja, se pegarmos os municípios com grandes áreas, quanto do país conseguiríamos preencher com 12 milhões de habitantes?
O interessante é que essa questão recai exatamente no problema da mochila, que é um famoso desafio de programação inteira. Depois de estudar profundamente no wikipedia (😄), vi que o problema não é tão trivial como parece.
O problema da mochila
Considere o seguinte contexto: você tem uma mochila com capacidade de 15kg e precisa carregar a combinação de itens com maior valor, com cada item possuindo valores e pesos diferentes.
Outra forma de pensar nesse problema é com um cardápio de restaurante:
Em linguagem matemática, o que temos é a task:
\[ \begin{aligned} & \text{maximizar } \sum_{i=1}^n v_i x_i \\ & \text{sujeito à } \sum_{i=1}^n w_i x_i \leq W, \text{ com } x_i \in\{0,1\}\\ \end{aligned} \]
No nosso caso essas letras significam isso aqui:
- \(n\) é o número de municípios no Brasil (5570).
- \(v_i\) é a área do município \(i\).
- \(w_i\) é a população do município \(i\).
- \(W\) é a população de São Paulo (12 milhões).
- \(x=(x_1,\dots,x_n)^\top\) é o vetor que seleciona os municípios. Se o município \(i\) faz parte da solução \(x_i=1\) e, caso contrário, \(x_i=0\).
Ou seja, queremos escolher municípios para colocar na mochila tentando maximizar a área, mas o máximo de população que podemos contemplar é 12 milhões.
O problema da mochila é muito interessante pois trata-se de um problema NP-difícil, ou seja, não existe um algoritmo de polinomial capaz de resolvê-lo. Se \(w_i > 0, \forall i\in1,\dots,n\) então a solução pode ser encontrada com um algoritmo pseudo-polinomial.
Forma ad-hoc
Se \(x_i\) pudesse assumir valores entre zero e um (ou seja, se pudéssemos selecionar apenas pedaços de municípios), a solução seria trivial. Bastaria colocar os municípios em ordem decrescente pela razão \(v_i/w_i\) e escolher os municípios ou parte deles até obter \(W\).
Isso indica uma forma sub-ótima de resolver o problema. Chamamos essa solução de ad-hoc. A solução é encontrada assim:
- Colocar os municípios em ordem decrescente pela razão \(v_i/w_i\),
- Escolher os municípios de maior razão até que a população do próximo município estoure \(W\).
- Escolher outros municípios com maior razão na ordem até não ser possível incluir mais nenhum município.
Solução ótima
A solução ótima pode ser encontrada usando a função mknapsack() do pacote adagio. Por exemplo, considere os vetores de pesos w, valores p e máximo cap abaixo.
p <- c(15, 100, 90, 60, 40, 15, 10, 1)
w <- c( 2, 20, 20, 30, 40, 30, 60, 10)
cap <- 102O vetor-solução é dado por
is <- adagio::mknapsack(p, w, cap)
is$ksack[1] 1 1 1 1 0 1 0 0Dados
As áreas e estimativas das populações dos municípios do Brasil em 2010 foram obtidas dos pacotes {geobr} e {abjData}. A leitura é realizada usando pacotes do {tidyverse}.
Pacotes:
library(magrittr)
library(sf)da_sf <- geobr::read_municipality(year = 2010)
dados <- da_sf %>%
dplyr::mutate(area = as.numeric(sf::st_area(geom)) / 1e6) %>%
tibble::as_tibble() %>%
dplyr::select(-geom) %>%
dplyr::mutate(muni_id = as.character(code_muni)) %>%
dplyr::inner_join(
dplyr::filter(abjData::pnud_min, ano == "2010"),
"muni_id"
) %>%
dplyr::select(muni_id, area, pop) %>%
dplyr::mutate(razao = area / pop) %>%
dplyr::filter(area > 0)Resultados
A solução ad-hoc e ótima são computadas com esse código:
d_solucao <- dados %>%
dplyr::arrange(dplyr::desc(razao)) %>% # ordena para solucao adhoc funcionar
dplyr::mutate(
area2 = as.integer(area * 1000), # necessario para mknapsack funcionar
s_knapsack = adagio::mknapsack(area2, pop, max(pop))$ksack,
acu = cumsum(pop),
s_adhoc0 = dplyr::if_else(acu < max(pop), 1, 0),
s_adhoc = s_adhoc0
) Agora, vamos melhorar a solução ad-hoc incluindo os melhores municípios.
id_melhor <- 0
pop_faltam <- with(d_solucao, max(pop) - sum(s_adhoc0 * pop))
while (is.na(id_melhor)) {
# pega id do melhor municipio a ser incluido
id_melhor <- with(d_solucao, which(pop <= pop_faltam & s_adhoc == 0)[1])
if (is.na(id_melhor)) {
d_solucao$s_adhoc[id_melhor] <- 1
pop_faltam <- with(d_solucao, max(pop) - sum(s_adhoc * pop))
}
}A Tabela abaixo mostra os municípios que foram classificados diferentemente nos dois métodos. Note que a solução ótima trocou apenas um município da solução adhoc (Nova Aurora - GO) pelo município de Monte Alegre de Minas - MG.
d_solucao %>%
dplyr::filter(s_adhoc != s_knapsack) %>%
dplyr::inner_join(abjData::muni, "muni_id") %>%
select(uf_nm, muni_nm, area, pop, s_adhoc, s_knapsack) %>%
knitr::kable(caption = 'Municípios diferentes nas duas soluções.')| uf_nm | muni_nm | area | pop | s_adhoc | s_knapsack |
|---|---|---|---|---|---|
| Piauí | Colônia Do Piauí | 949.0047 | 7387 | 0 | 1 |
| Tocantins | Riachinho | 517.6699 | 4030 | 0 | 1 |
| Santa Catarina | Palmeira | 289.4767 | 2291 | 0 | 1 |
A Tabela abaixo mostra a diferença dos resultados dos dois métodos. A solução ótima fica com apenas 92 pessoas a menos que São Paulo.
| Método | Área total | População total | Diferença para sp |
|---|---|---|---|
| adhoc | 5669732.52073351 | 11152637 | 13906 |
| knapsack | 5671488.67201654 | 11166345 | 198 |
| São Paulo | - | 11166543 | 0 |
Mapa final
Visualmente, a solução ótima e a solução adhoc são idênticas. Por isso vou mostrar apenas como fica o mapa para a solução ótima.
O resultado aparece na Figura 1. É realmente impressionante ver que aquela regiãozinha vermelha tem a mesma população que toda a região azul do mapa.
da_sf %>%
dplyr::mutate(muni_id = as.character(code_muni)) %>%
dplyr::inner_join(d_solucao, "muni_id") %>%
ggplot2::ggplot() +
ggplot2::geom_sf(
ggplot2::aes(fill = as.factor(s_knapsack)),
size = 0
) +
ggplot2::geom_sf(
fill = "red",
size = 0,
colour = "black",
data = dplyr::filter(da_sf, code_muni == "3550308")
) +
ggplot2::scale_fill_manual(
values = c("gray90", viridis::viridis(1, 1, .2, .8))
) +
ggplot2::theme_void() +
ggplot2::theme(legend.position = "bottom") +
ggplot2::labs(fill = "Solução")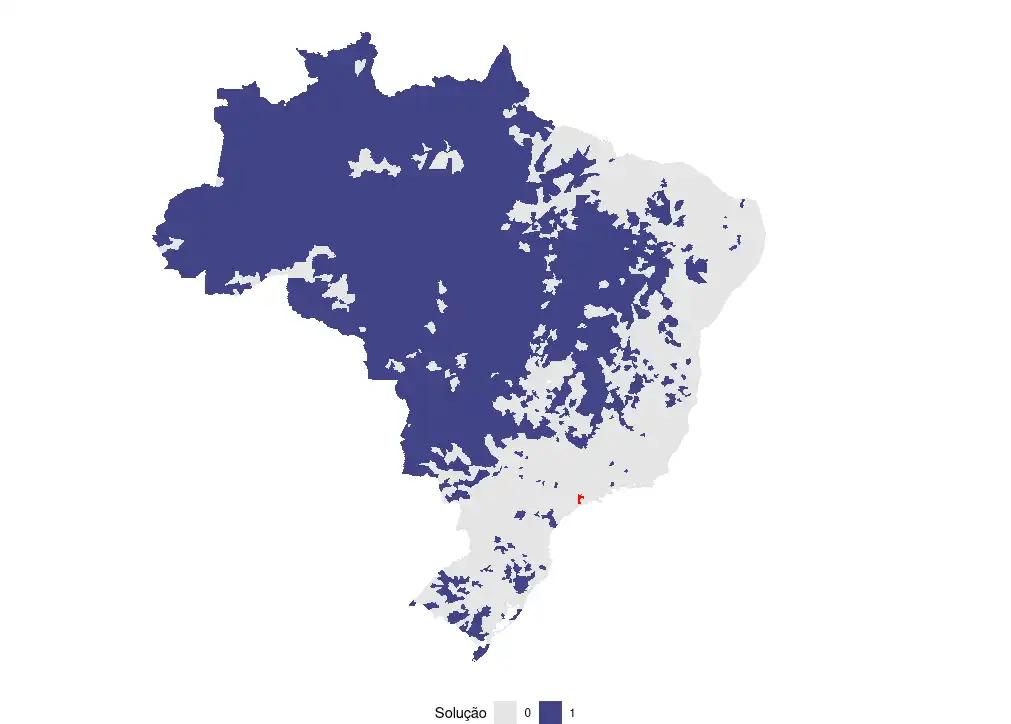
Figura 1: Resultado final da análise. A área em azul tem a mesma população da área em vermelho!
É isso! Happy coding ;)


